Assignment 1: Exploring Graphs of the a Similar Equation

By: Mary Wisniewsky

Exercise: We're going to explore many graphs of the following equation:

First, let's graph this equation when n=2.

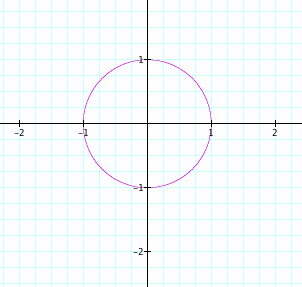
When we graph the equation when n=2, we come up with a circle. This should make sense since that would make one of the standard equations for a circle. When we rearrange the equation to let it equal to y, we get the distance formula from point (0,0) from any distance 1 unit away from the point.

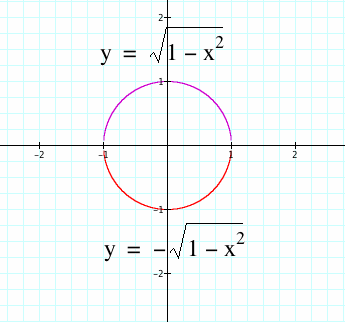
Now, what should happen when we set n=3? Will it be similar to when n=2?

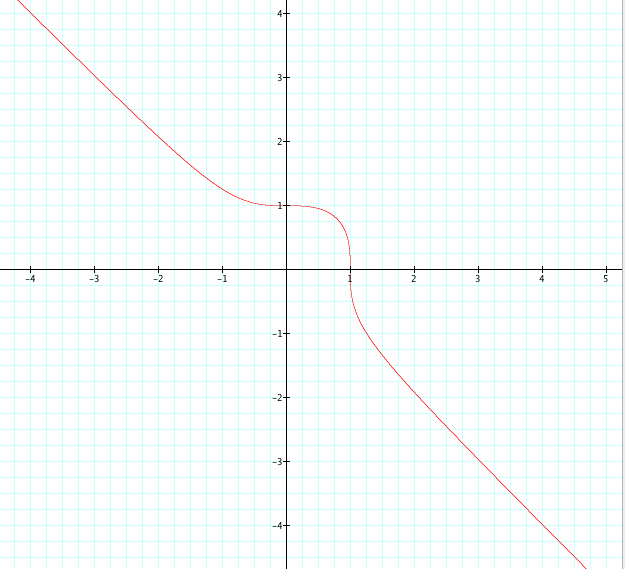
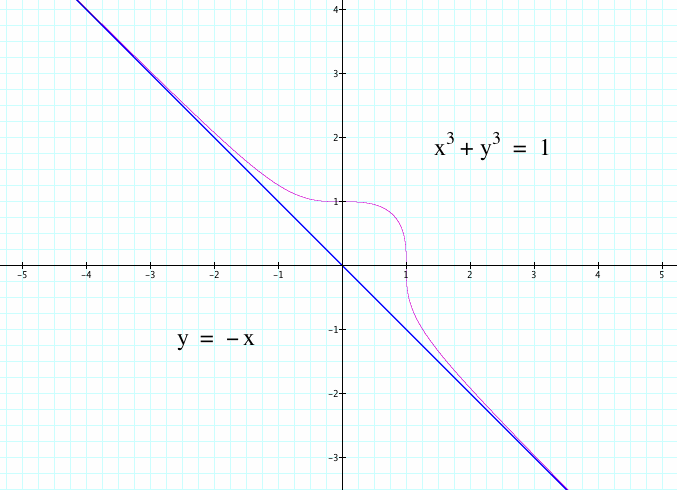
In this graph we have an entirely different shape than when n=2. The graph retains a similar shape around 0<x<1, but then curves out to run along the line y=-x (we will come back to this idea later in the assignment).

Now will the graph be similar or different from when n=2 or when n=3 for the equation when n=4?

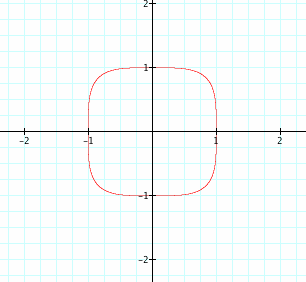
This graph of the equation is similar to when n=2 but the shape is stretched. What are we going to see now when n=5?

This graph is very similar to when n=3, but just slightly stretched.

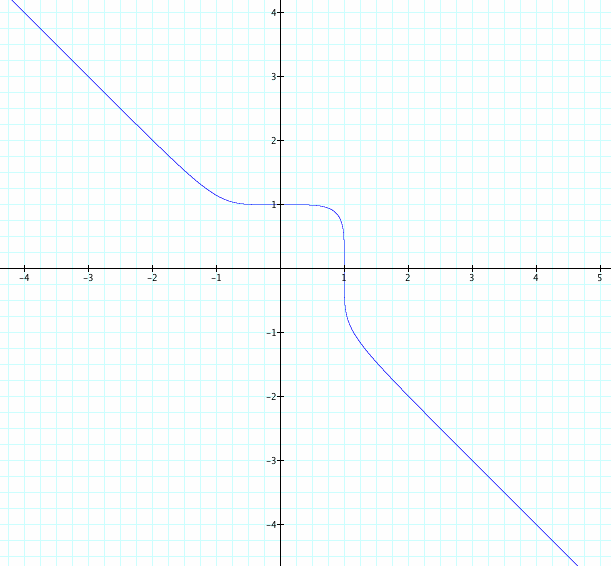
Here are the four graphs on the same cartesian plane:

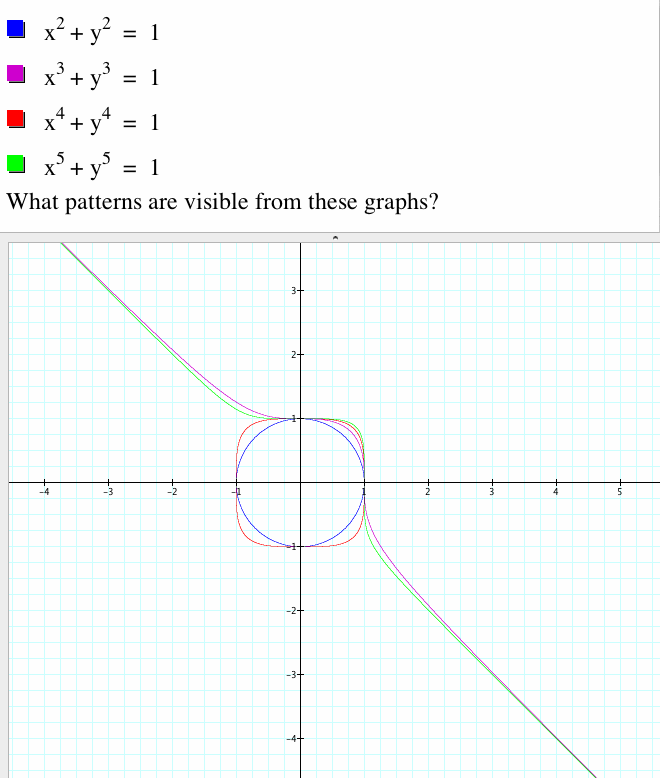
As n increases and is even, the shape starts as a circle and continues to stretch. However as n increases and is odd, it remains similar to when n=3, but the region near 0 < x < 1 continues to stretch as the rest of the graph almost becomes into the line y= -x where y=-x becomes an asymptote.

So why do the odd graphs during this interval have an asymptote of y= - x? Let's take a look at a point the is in this region. When we replace x and y with 4 and - 4 respectively into the equation, we get

which this does not work for our original equation. Therefore the shape of the graph will not touch the line y= -x.

Now that we have found this pattern, what should we expect to see when n=24 and when n=25? Explore the following animation to find out if the pattern remains true! (Notice when n is not an integer, what happens to the graph?)

In conclusion, there are many observations that can be concluded from varying the exponent of this equation and how patterns can be found everywhere in mathematics!

Return back to the Mary Wisniewsky's main page