Assignment 2: Quadratics Adventure

By: Mary Wisniewsky

We are going to explore the following quadratic equation and its many properties:

Let's take a look at the graph of this equation when d=f=1:

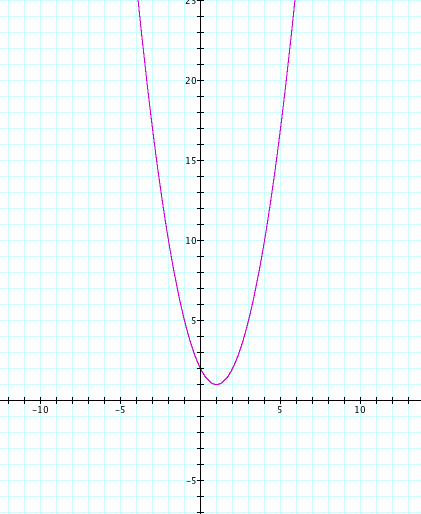
Here we have a quadratic equation with the vertex (1,1). How does the vertex correlate to our given equation? Let's keep exploring.

Take a look at the following graphs. We are going to keep f fixed and vary the placement of d:

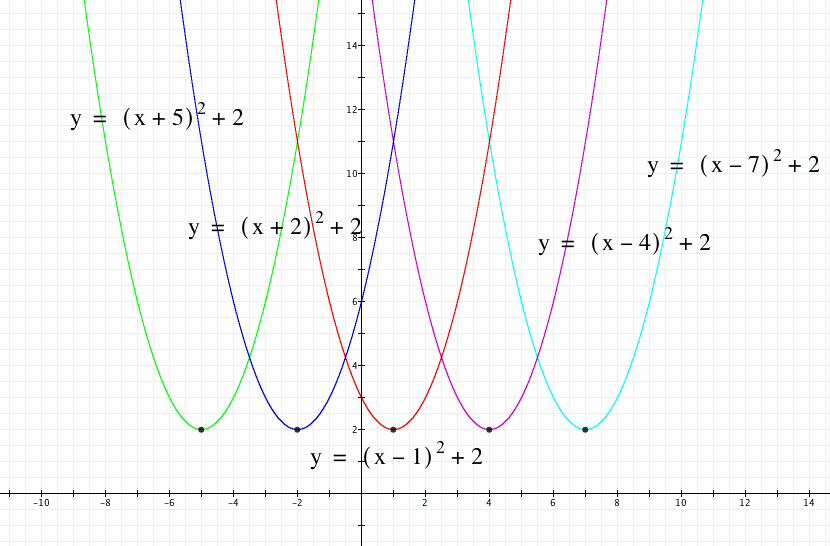
As you can see from the graphs, as d changes, the original graph when d=1, f=2, undergoes a horizontal translation.

Now let d remain constant and vary the value of f. What is going to change? The graphs should look something like this:

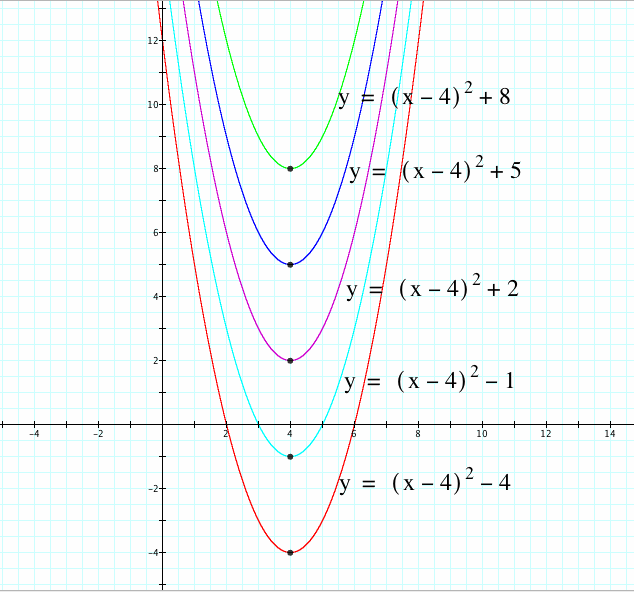
Instead of a horizontal translation, when f is varied, the graphs vertically translate.

Now after examining these graphs, how can we find our vertex from the equation?

Along with graphing the original equation, graph when d=4, f=1

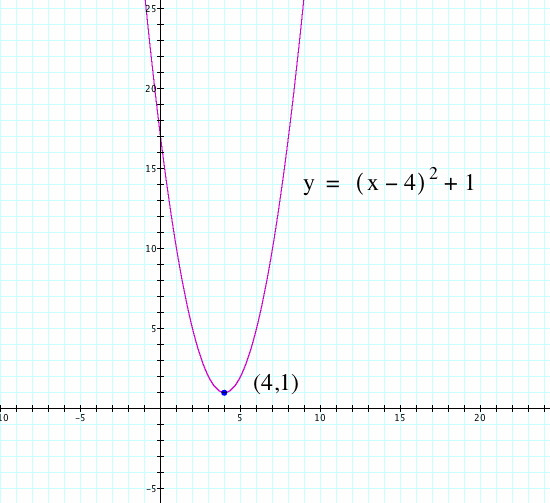
From this graph and the previous graphs formed, we can conclude that: (d,f) is the vertex for the original equation, when d is varied the graph translates horizontally, and when f is varied the graph translates vertically. Explore this video to see the translations of d and f! (Which graph represents varying d and which one represents varying f?)

Check out the translations of the original graph when its set equal to z!

Return to Mary Wisniewsky's Main Page