Assignment 4: Centers of Triangles

By: Mary Wisniewsky

Exploration in GSP tools and centers of a triangle!

There are four main centers of a triangle that we are going to study in this assignment:

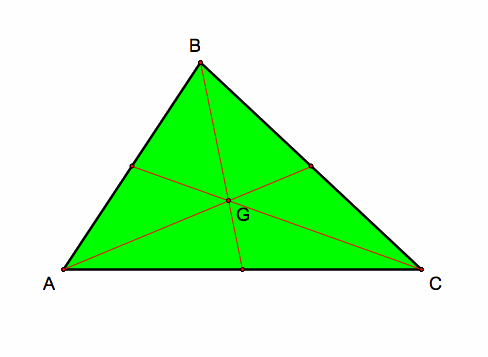
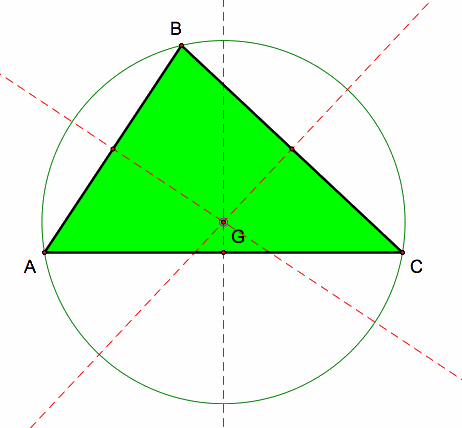
1.) The Centroid of a triangle is the intersection point between the three medians of a triangle. The centroid is always labeled as point G on the plane of the triangle. Here is the centroid and the three medians of triangle ABC:

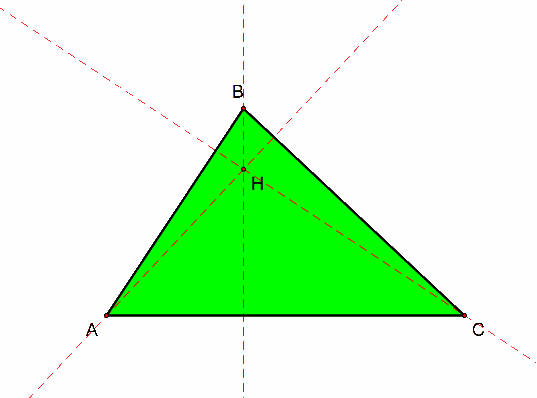
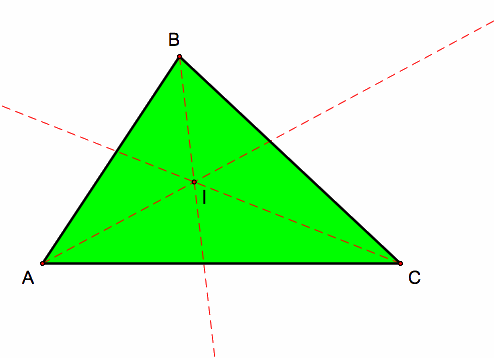
2.) The Orthocenter of a triangle is the common intersection point between the altitude lines of a triangle. The orthocenter is always labeled as point H on the plane of the triangle. Here is the orthocenter and altitude lines of triangle ABC:

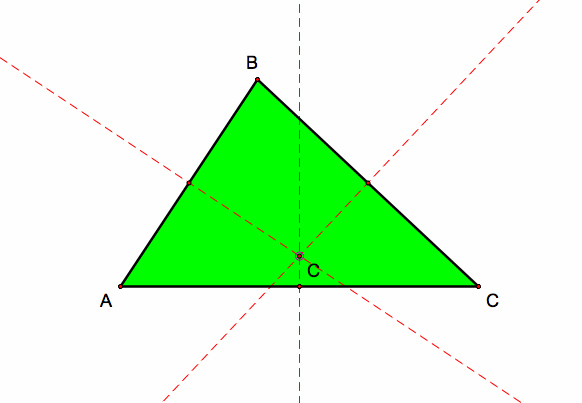
3.) The Circumcenter of a triangle is the center equidistant from all the vertices in the triangle and is on the perpendicular bisectors of the triangle. The circumcenter is always labeled as point C on the plane of the triangle and it is the center of the circumscribed circle (The circumcircle is the circle that includes all three vertices of the triangle on the circle) of the triangle. Here is the circumcenter and corresponding perpendicular bisectors of triangle ABC and the circumcircle of triangle ABC:

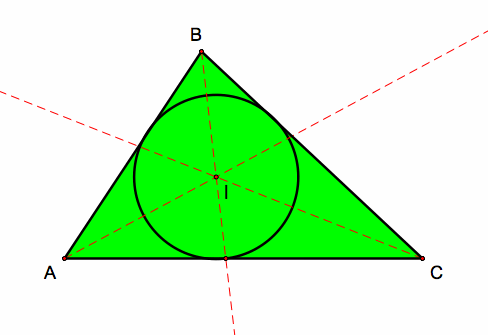
4.) The Incenter of a triangle is the intersection point of the angle bisectors of each angle inside the triangle, and lies interior in the triangle in which it is equidistant from each vertex of the triangle. This point is always labeled as point I. The incenter is also the center of the incircle (inscribed circle) of the triangle. Here is the incenter and the incircle for triangle ABC:

(To use various triangle center GSP scripts, use some of the tools on this page).

When we display all of these four triangle centers on triangle ABC, we get:

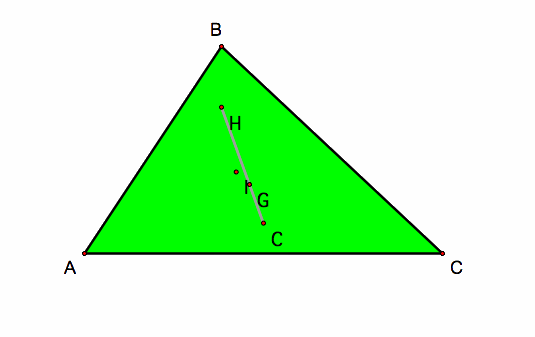
The centers G, H, and C form a line called the euler line.

(Explore this GSP link to move each vertex of the graph to show how the euler line remains intact).

Another interesting tool with centers and triangles is forming the nine-point circle (with center N). The nine point circle of a triangle includes:

1.) midpoints of a triangle.

2.) feet of the altitudes of a triangle.

3.) The three midpoints of the altitude segments in between the orthocenter and the respective vertices.

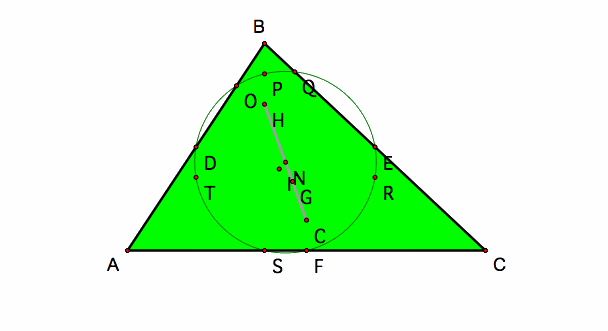
This is the nine-point circle for triangle ABC. Points D,E,F are the midpoints of the triangle, points O,Q, and S are the feet of the altitudes of the triangle, and points P, R, and T are the midpoints of the altitude segments in between the orthocenter and the respective vertices.

Notice the center N of the nine-point circle. It lies directly on the euler line along with centers, G,H, and C.

Also an interesting triangle is a medial triangle. This formed by connecting the midpoints of any triangle and you get a new triangle with the midpoints as the vertices.

Let's look at the medial triangle for triangle ABC:

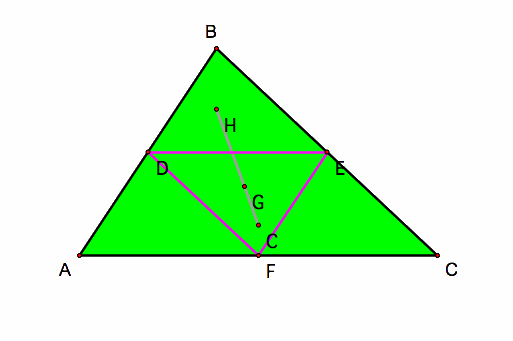
Above we have the triangle ABC with the Medial triangle formed by connecting the midpoints D, E, F to form triangle DEF.

Let's observes the triangle centers of triangle DEF and compare with its original triangle ABC:

Centroid

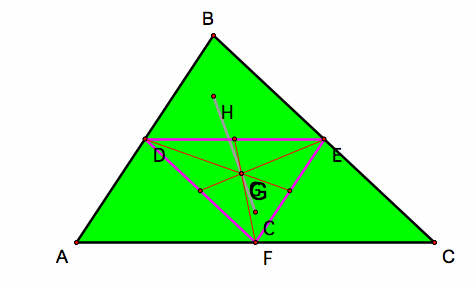
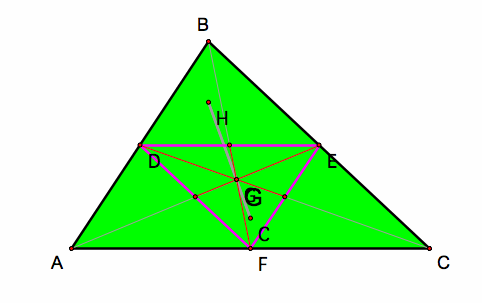
The centroid G of triangle DEF is same point for the Centroid G of triangle ABC. Examine the triangle on the right.

Notice how the medians for triangle DEF intersect with the medians of triangle ABC to have the same intersection point of the medians.

Orthocenter

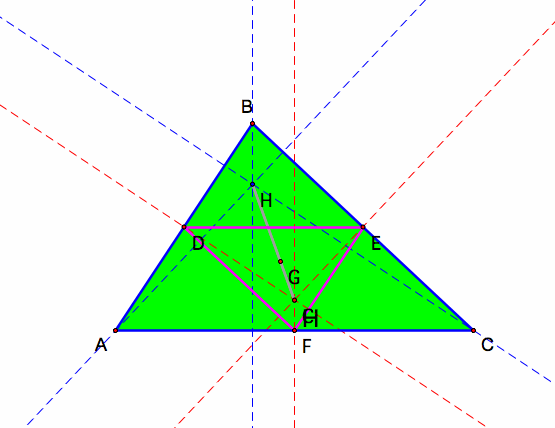
In this case, the orthocenter for triangle DEF is the circumcenter for triangle ABC.

The altitude lines of each triangle seem to run parallel to each other as well.

Circumcenter

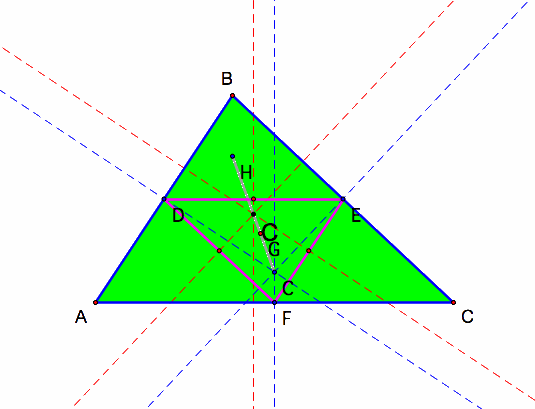
The Circumcenter for triangle DEF is not the same point as the circumcenter for Triangle ABC,

however this circumcenter lies still on the euler line.

Also these perpendicular bisector lines seem to also run parallel to each other.

Incenter

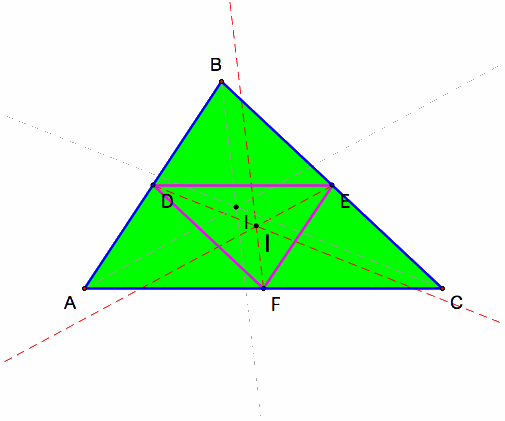
The incenters for these triangles are also not the same and neither line on the Euler line.

However, like the case for the orthocenter and circumenter, these angle bisectors lines for each triangle seem to run parallel to each other.

After learning about the four main centers of a triangle, the nine-point circle, and the medial triangle,

I hope this can better help explore many properties of a triangle and help with future geometric constructions.

Return to Mary Wisniewsky's Main Page