Assignment 6: A Three-Point Problem

By: Mary Wisniewsky

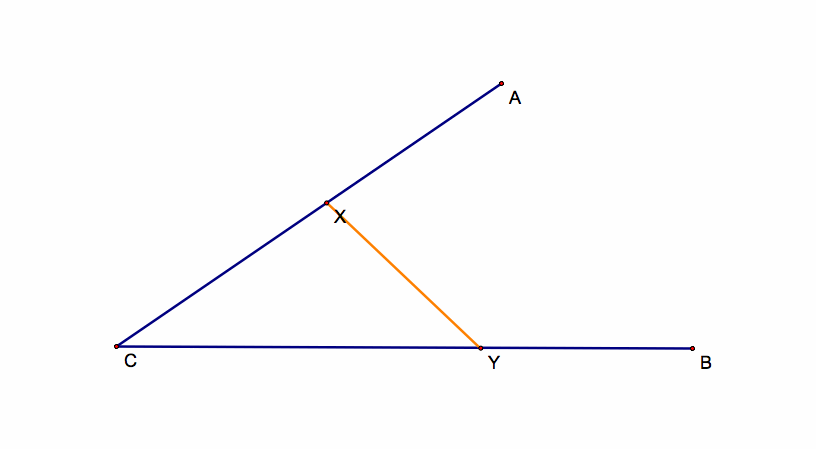
Problem: Given three points A, B, and C, draw an intersecting AC in the point X and BC in the point Y such that

AX=XY=YB

At the end of this exercise, our end picture should resemble this:

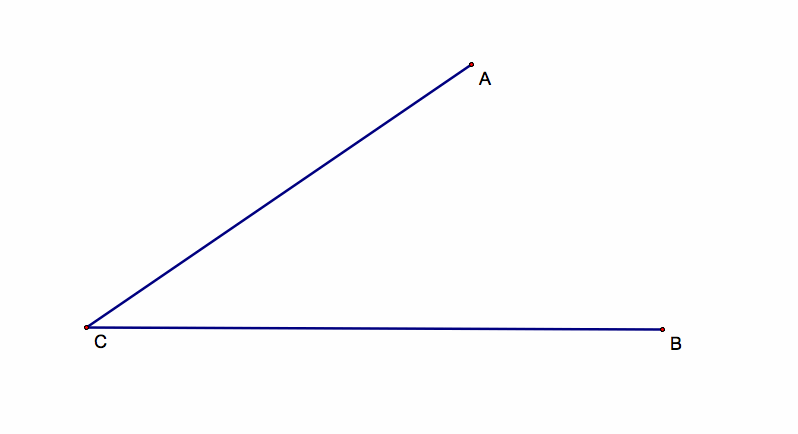
Let's start with our three points A,B, C and then we will have something like this picture:

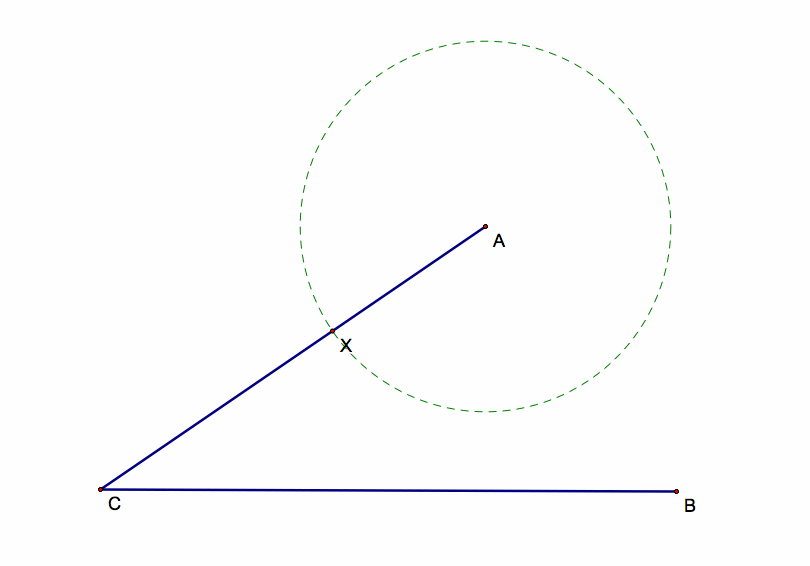
Now let's make a circle centered at point A such that it has a radius of length AX.

Now we need to make the same circle, but centered at point B.

It needs to have the same radius length as Circle A, because our end result needs to contain equivalent lengths such that AX=BY=XY.

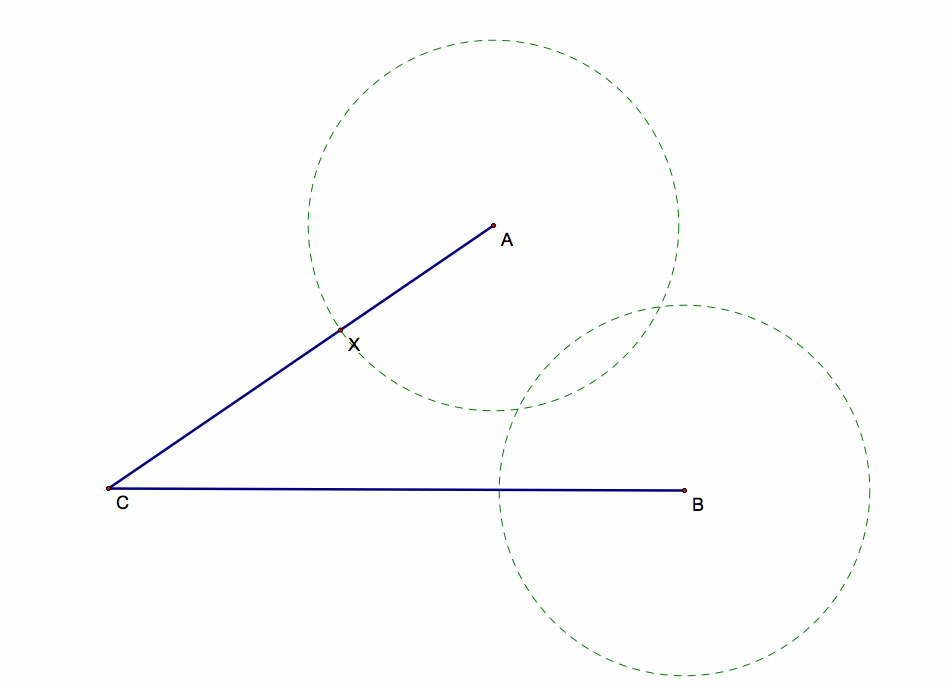
Once we have these two circles centered at A and B,

then we need to form one more circle centered At point X with the radius length equivalent to circles A and B.

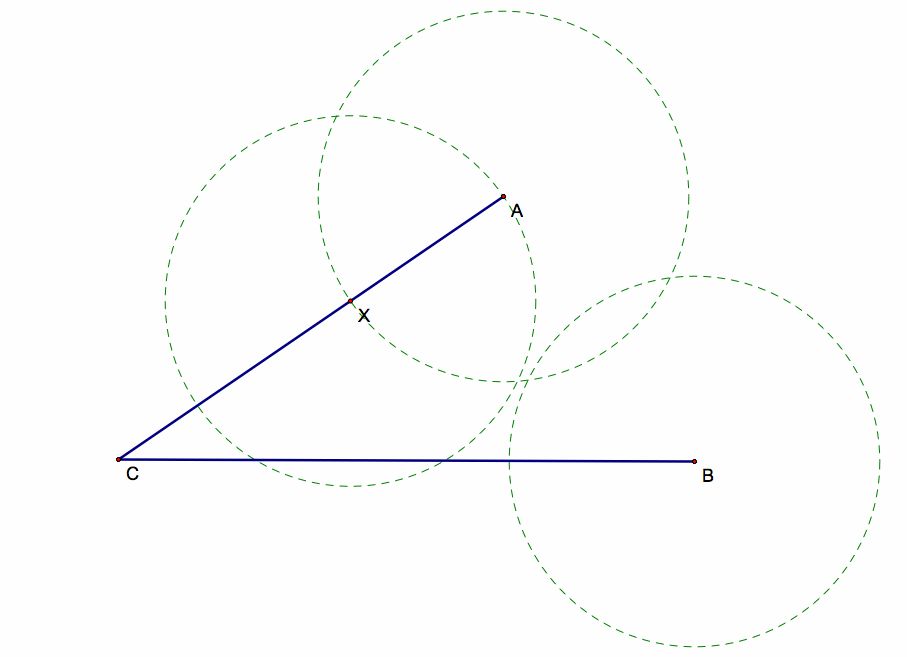
Once we have our three circles, we need to use the drag option on GSP.

We need to drag point X such that the circles X and B are intersecting at the same point on line BC.

This intersection point will be point Y.

These two circles need to be intersecting at the same point on BC, so that we know for sure the distance from X to Y is equivalent to the distance from this point Y to B

since the radii for all of are circles are equal to length of AX.

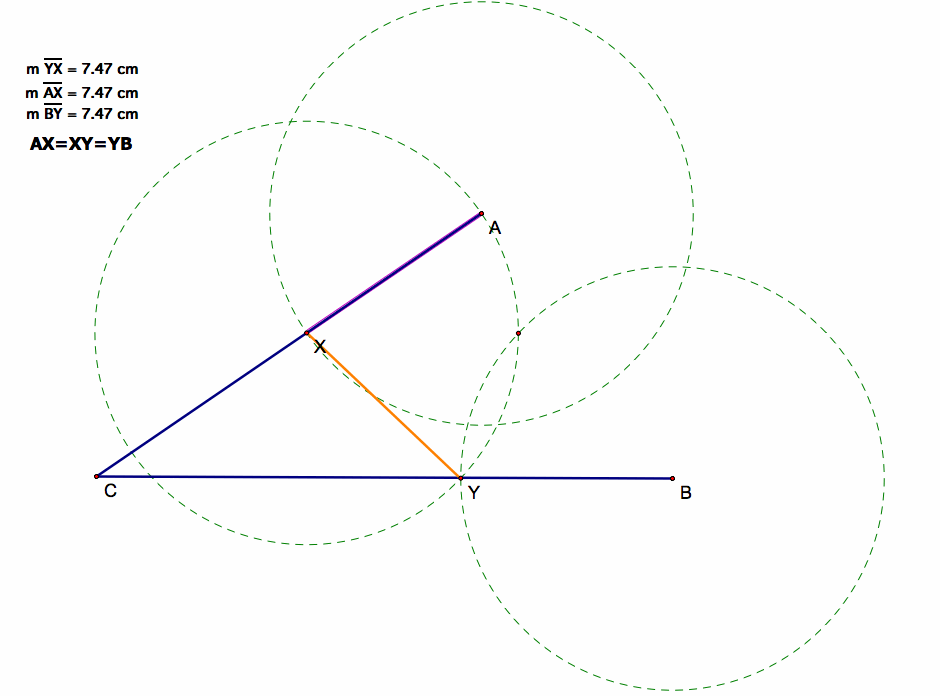
After measuring the lengths of AX, YX, and BY, you can see that they are all equal and should be from our circle constructions.

We have come to our end picture where AX=XY=BY for given point A,C, B.

Return to Mary Wisniewsky's Main Page