Assignment 7: Tangent Circles

By: Mary Wisniewsky

We are going to explore many properties of a tangent circle. A tangent circle is a circle tangent to two other circles.

For this exploration, we need to construct two circles. Let one of them be slightly larger than the other circle which lies inside of the circle.

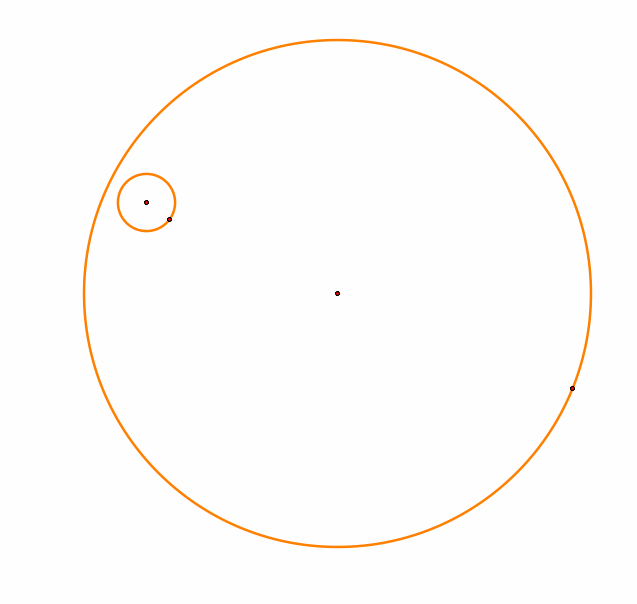
Construct a point on the larger circle other than the the point used to form the circle.

Then construct a line through the center and this new created point.

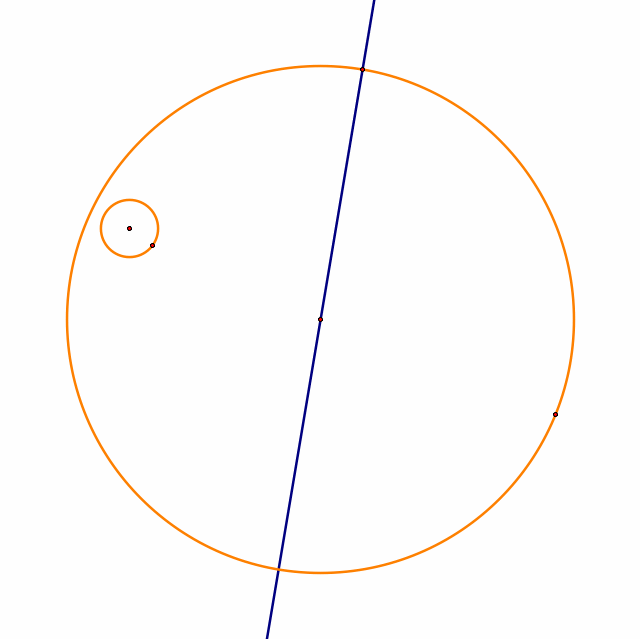
Make a circle centered at the newly constructed point on the larger circle and has a radius of the small circle.

Let this circle be a different color other than the circles we're using to form a tangent circle.

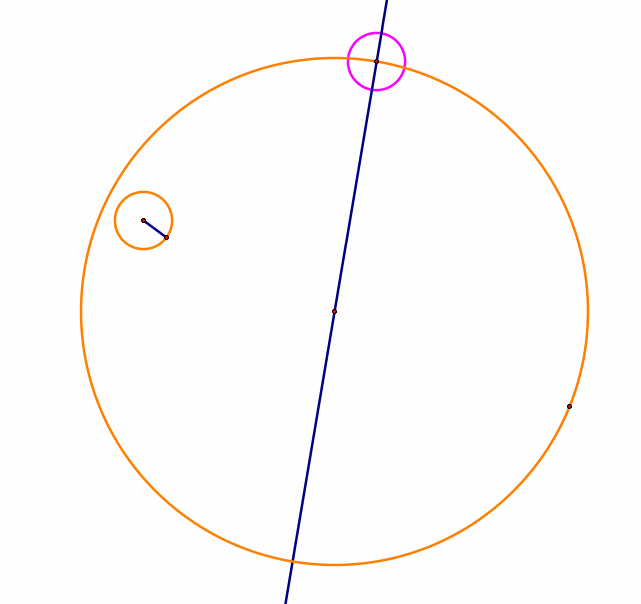
Construct the intersection point (outside of the orange circle) of the blue line and the pink circle.

Then connect this intersection with the center of the small orange circle by making a line segment.

Find the midpoint of this segment and construct the perpendicular line that is perpendicular to the midpoint and line segment.

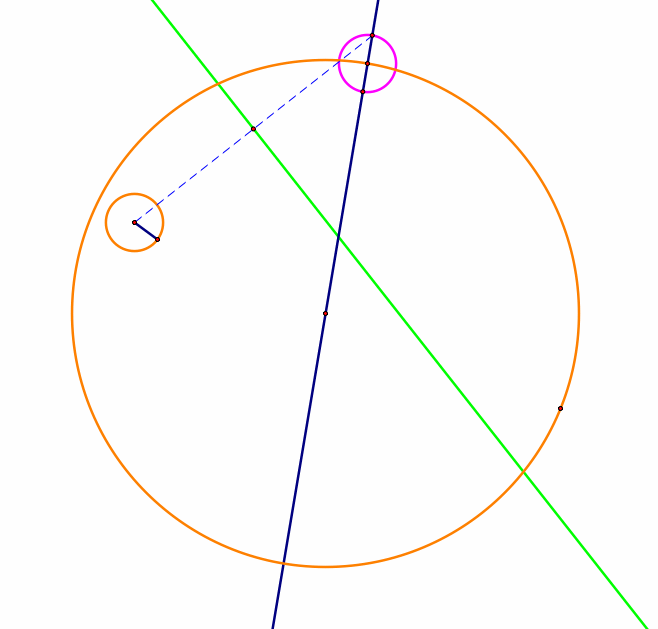
The intersection of the blue line and the perpendicular line is the center for our tangent circle.

Construct the tangent circle with center at the intersection point and point on the larger circle (center of the pink circle).

Let the tangent circle be colored differently so that it can stand out.

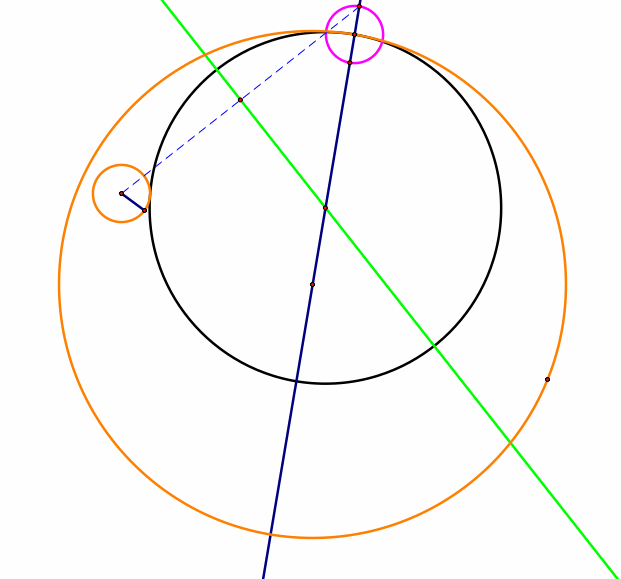
Let's examine some of the loci relating to this tangent circle.

Let's rotate the center of the pink circle around the large circle while we trace the center of tangent circle.

What should we see when we trace the locus of the center of the circle tangent to the original two circles?

When our original circles are inside of the other,the locus of the center of the circle tangent to the original two circles forms an ellipse.

Notice how the perpendicular formed is tangent to the locus. When the locus was traced, that line always ran tangent to the locus.

(See script tools at the end of the assignment)

When the perpendicular line is also traced, an envelope of lines is constructed and is all tangent to the ellipse.

Also when the midpoint of the segment formed by connecting the center of the small circle to the point on the larger circle is traced along with the center of the tangent circle, the locus of this midpoint results in a circle.

This correlates to the fact that when the point on the larger circle is being rotated around the circle, half the distance of the line segment would generate the radius of a circle.

Now instead of having one of the circles being inside of the other, let both original circles be disjoint.

Now the pink circle here is the tangent circle.

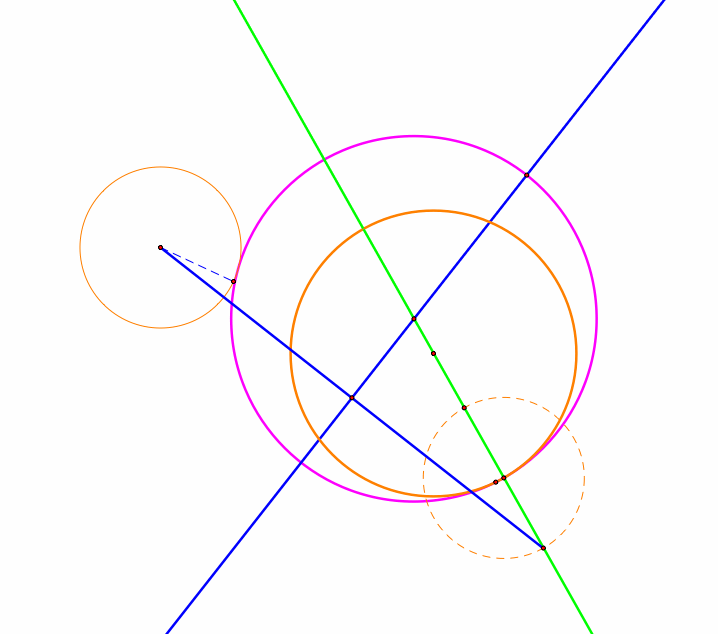
Similarly trace the center of tangent circle to generate the shape of the locus.

Are we going to see an ellipse again?

For this case we have an hyperbola instead of an ellipse and similarly take a look at when the perpendicular line is traced.

Will we also get a circle when we trace the midpoint of the segment?

Not only do we get a circle generated, but the circle lies tangent to the hyperbola traced when finding the locus of the center of the tangent circle.

Use this GSP link to explore further options hands-on with the many script tools attached!

Return to Mary Wisniewsky's Main Page