

Assignment 8: Orthocenters and Nine Point
By: Mary Wisniewsky
We are going to explore geometric constructions associating with altitudes and orthocenters of a triangle ABC.
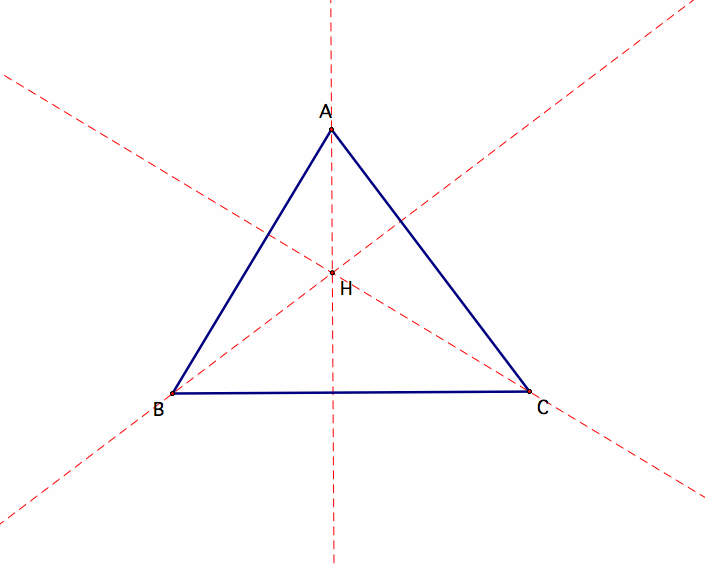
Construct the lines of the triangle that are perpendicular to the opposite side of the vertex.
Thus by definition, the orthocenter, H, is formed for triangle ABC.
Form precise triangles ABH (green), ACH (orange), and BCH (yellow). Find the orthocenters of each of these triangles.
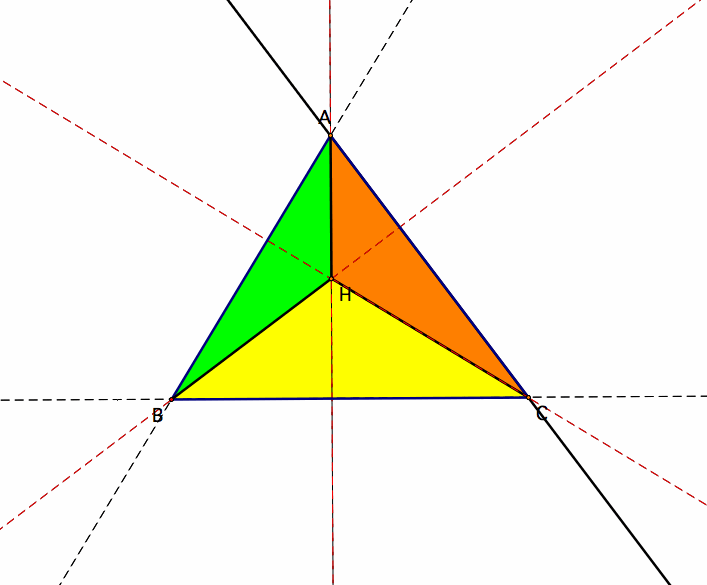
In the above image we have Triangle ABC, with subtriangles ABH, ACH, and BCH where H is the orthocenter of triangle ABC.
The black solid and dotted lines are the perpendicular lines opposite to each vertex for each triangle.
As you can see from the picture, the original orthocenter H is the orthocenter for all three of these subtriangles. How is this possible?
Remember the red lines are the perpendicular lines opposite of the vertices of triangle ABC. Line segments AH, BH, and CH exist on these perpendicular lines.
Therefore the perpendicular lines opposite to the vertices of the subtriangles (A, B, C) are going to intersect the line segments of the original triangle ABC
and the perpendicular lines opposite H intersect with the red perpendicular lines.
Now lets form the Circumcircle for ABC with center E which is the (circumcenter for triangle ABC).
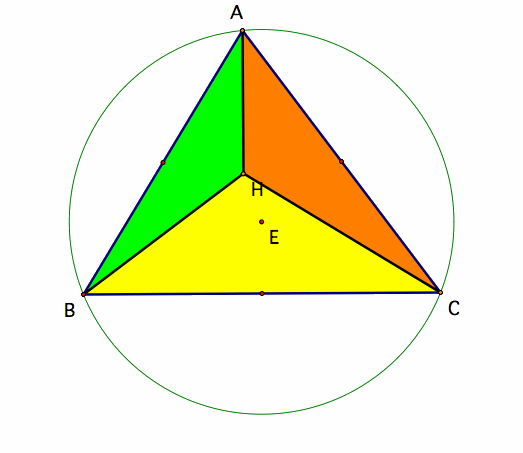
Also let's compare this circumcircle to the circumcircles for subtriangles.
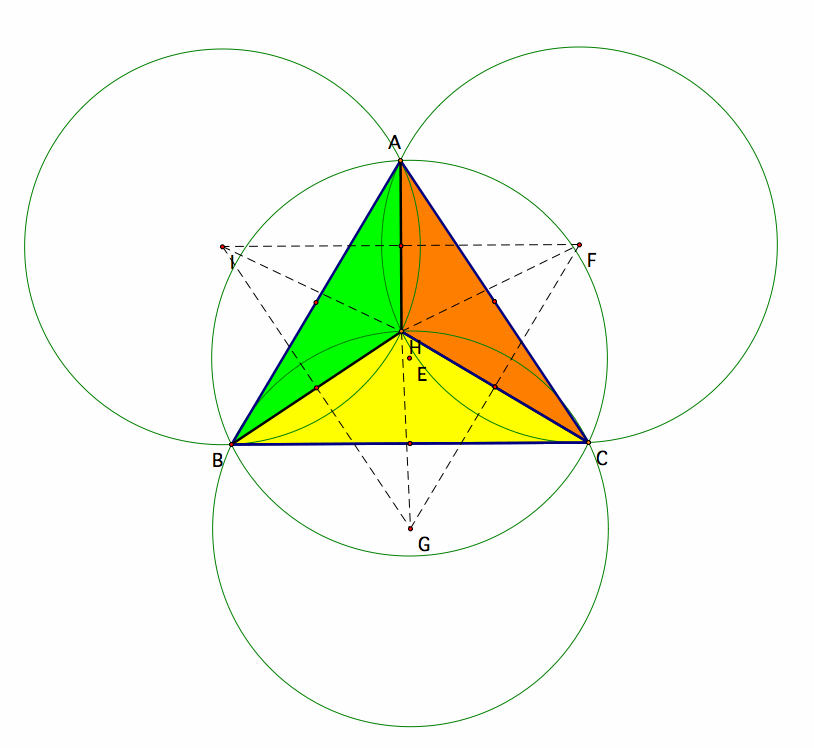
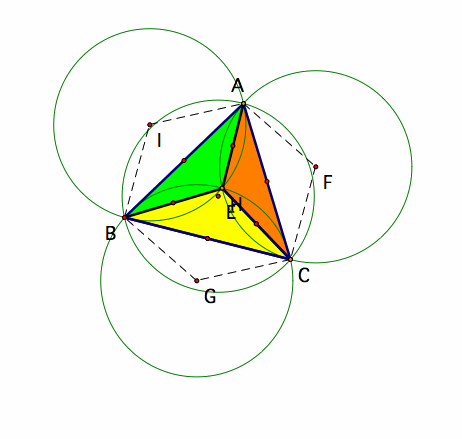
Notice from the above pictures that the circumcircles of the sub triangles are congruent to the circumcircle of the original triangle ABC and Triangle ABC is congruent to Triangle IGF.
Let the circumcircle of triangle ABC=Circle H, the circumcircle of triangle ABH= Circle I, the circumcircle of triangle ACH=Circle F, and the circumcircle of triangle BCH=Circle G.
The Radius for Circle H is equivalent to lengths of segments AH, BH, and CH.
The Radius for Circle I, F, and G is equivalent to the length of segments IH, FH, and GH respectively.
When you connect points A,B,C, F, G, I like the picture on the upper-right, the result is a 6 sided polygon.
What happens When one of the original vertices (A, B, C) is dragged to be on the orthocenter? Let B be positioned on H.
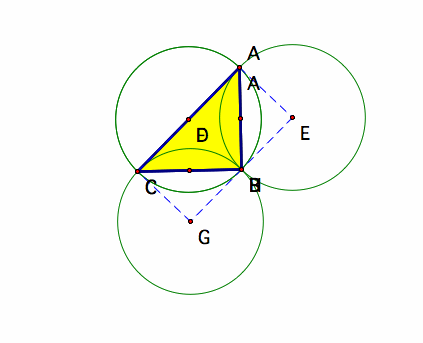
Instead of hexagon for the figure formed after connecting A,B,C to the centers of the circumcircles of the subtriangles,
we have a quadrilateral (rectangle) where the short legs are equivalent to the radii of the circumcircles and the long leg is the diameter of the circumcircles.
(Explore the gsp link to see what else can happen when vertices are moved).
Recall what the nine-point circle of any triangle is:
The nine point circle includes:
1.) midpoints of a triangle
2.) the feet of the altitudes of a triangle.
3.) The three midpoints of the altitude segments in between the orthocenter and the respective vertices.
Examine the Nine point circle for triangle ABC and compare to the nine point circle for the subtriangles.
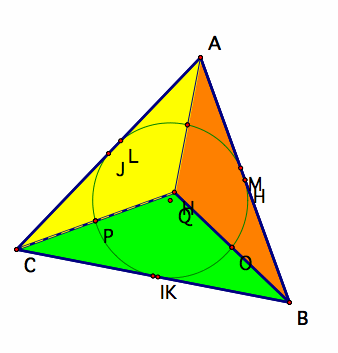
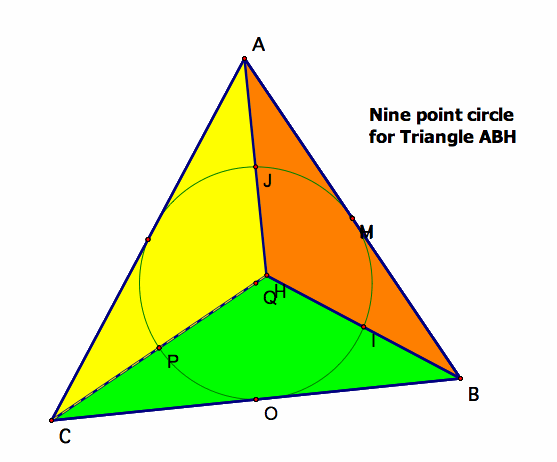
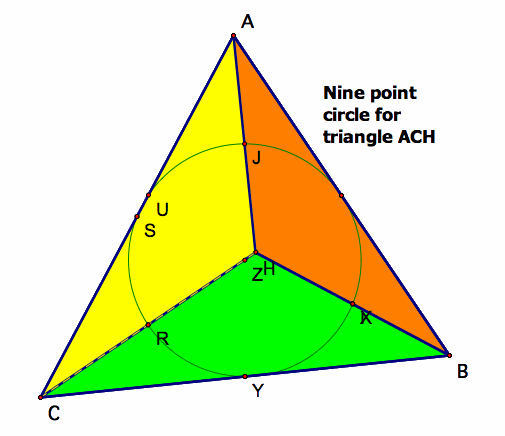
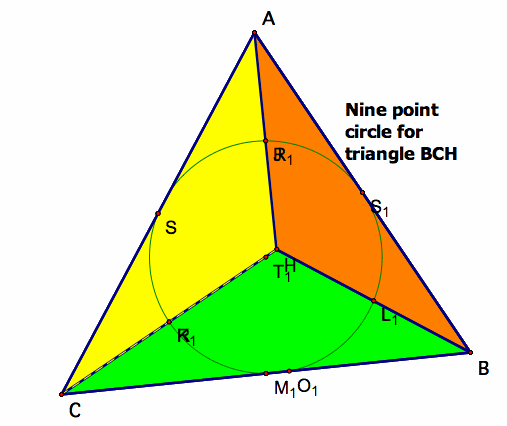
All of these nine-point circles are congruent to the original triangle's nine-point circle.
This correlates to the same conclusion we drew from all of the subtriangles having the same orthocenter as triangle ABC.
What other conclusions can be drawn from these nine point circles?
Use the following GSP script tools for the TRIANGLE ABC on GSP to see how the nine-point circles are all the same circle and how it is also the incircle for these triangles:
Return to Mary Wisniewsky's Main Page