Assignment 9: Pedal Triangles

By: Mary Wisniewsky

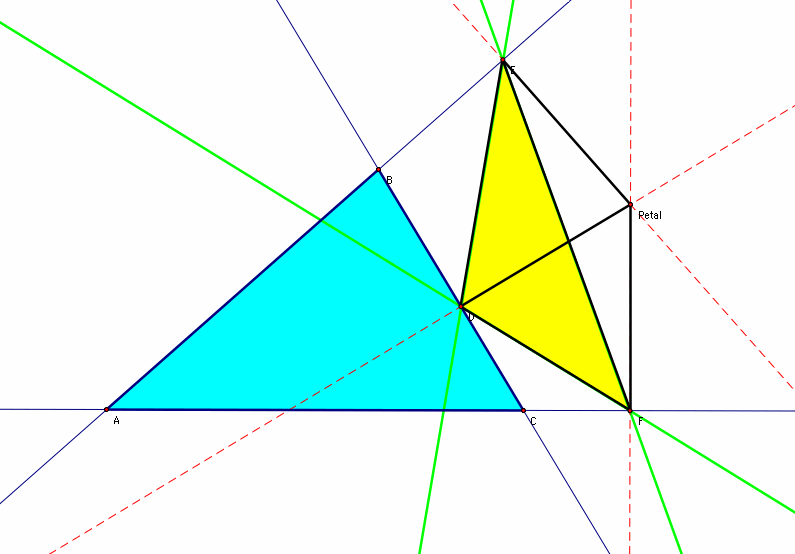
Given Triangle ABC and a pedal point (any point in the plane), a pedal triangle is the triangle DEF. This triangle consists of points D, E, F that are the intersection points of the lines perpendicular to the pedal point and the lines of the triangle ABC. A pedal point can lie outside or inside the original triangle ABC as well as being on one of the lines of the triangle ABC. The above picture includes the petal point existing outside of the triangle.

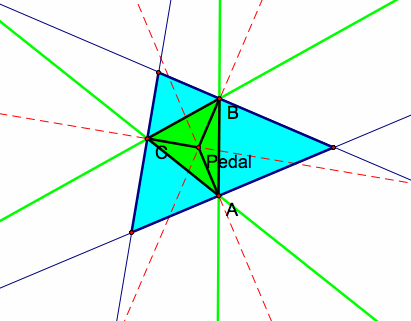
Here is a triangle ABC where the pedal point lies inside triangle ABC:

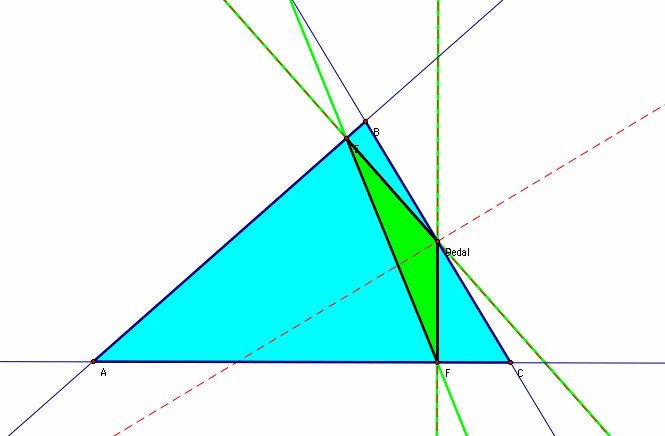
And, here is a case where the pedal triangle lies on one of the lines of the triangle:

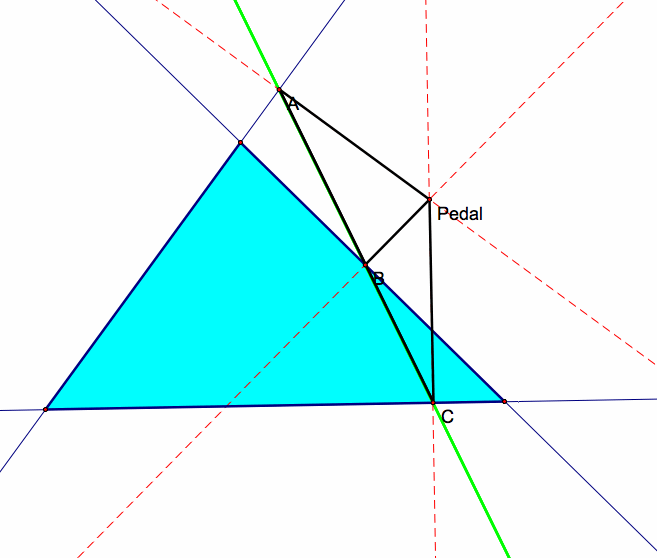
Also when all three vertices of the Pedal Triangle are collinear such that the triangle becomes degenerate,

the line created from this is called the Simson Line.

Let's take a look at a special case and its properties.

Draw the circumcircle of a triangle ABC which contains the circumcenter C.

Make a circle centered at C that has a radius slightly larger than the circumcircle.

Let the pedal point be contained on this new circle and make the midpoints of the Pedal triangle.

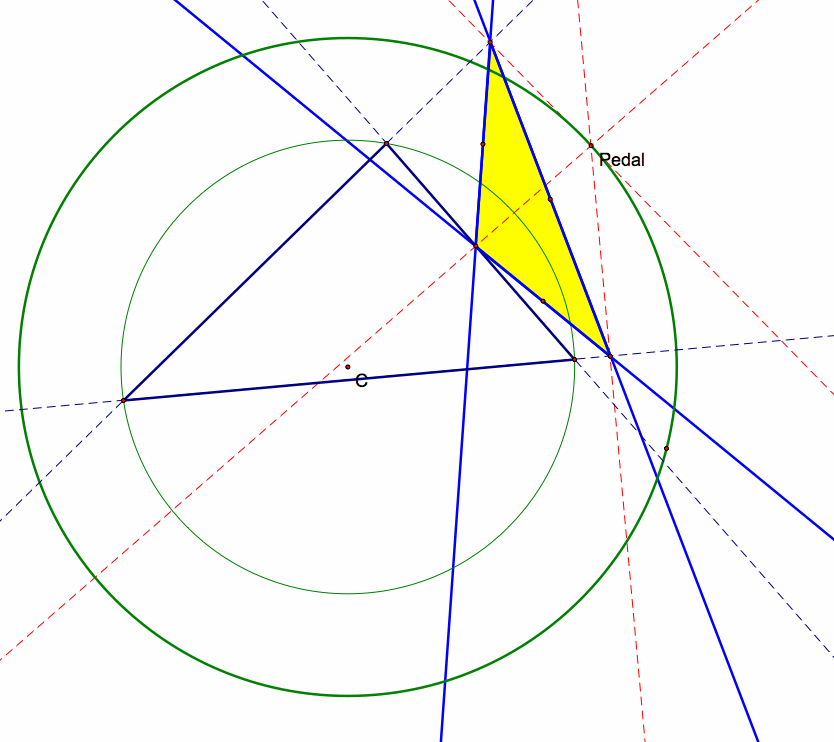
Let's take a look at what the locus of these midpoints might look like when we animate the pedal point and trace the midpoints.

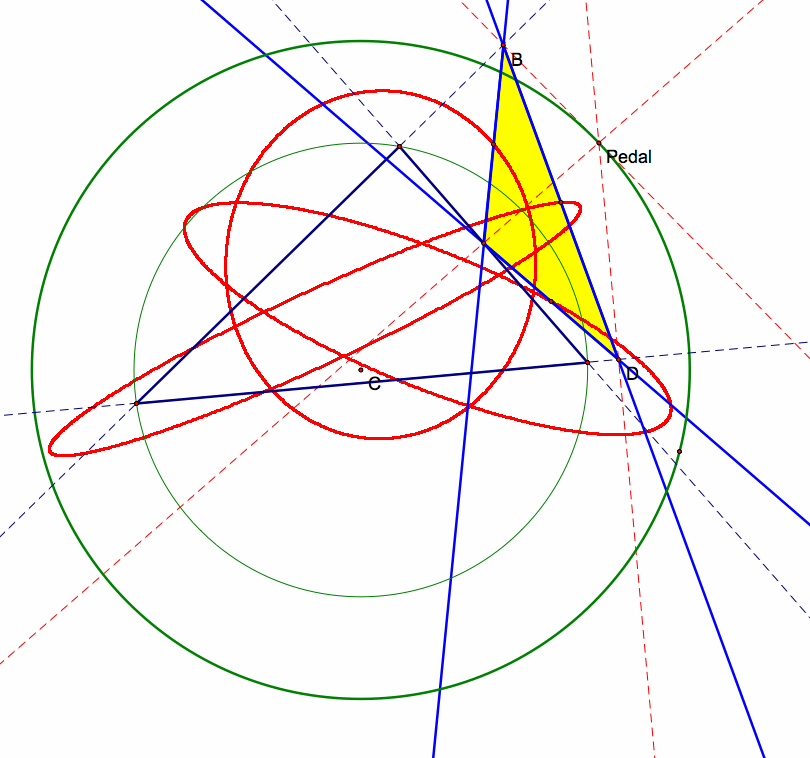
When you trace these points and let the pedal point circle around the larger circle, the locus of the midpoints of the pedal triangle are in red and are in the shape of ellipses.

Here are just some of the many explorations with pedal triangles. Use this script tool of a Pedal Triangle to continue other explorations.

Return to Mary Wisniewsky's Main Page