Consequences of Ceva's Theorem

Kate Berryman
cavaleri@uga.edu

*Please make sure your browser is maximized to view this write up;

Tomasso Ceva was an Italian Mathematicians at the turn of the 18th century. He discovered a beautiful theorem that was named after him.

Ceva's Theorem states that given any triangle △ABC, the segments from A, B, and C to the opposite sides of the triangle are concurrent precisely when the product of the ratios of the pairs of segments formed on each side of the triangle is equal to 1.

To see a proof of Ceva's Theorem click HERE.

There are many consequences of Ceva's Theorem. Below are just a few of them.

Centroid

The centroid is the point where the three medians of a triangle are concurrent.

Proof: First, take any △ABC.

Construct the midpoints on each side of △ABC.

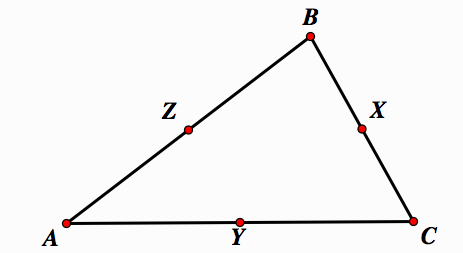
Construct segments from each vertex to the opposite endpoint.

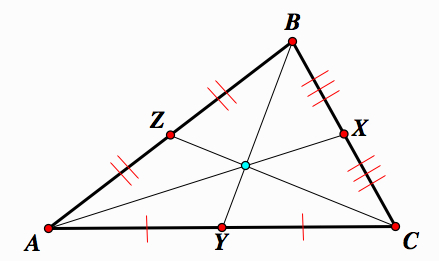
We know that AY = CY, AZ = BZ, and CX = BX. Therefore, 1/2 = AY = CY, 1/2 = AZ = BZ, and 1/2 = CX = BX. So,

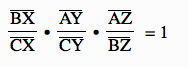
Therefore, the three medians of a triangle are concurrent at a point.

Circumcenter

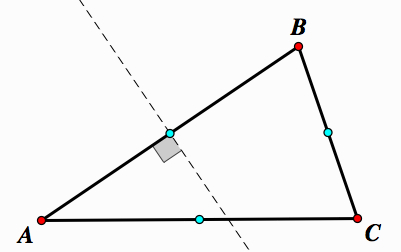
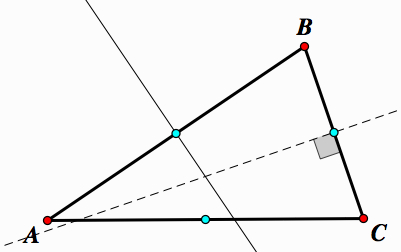
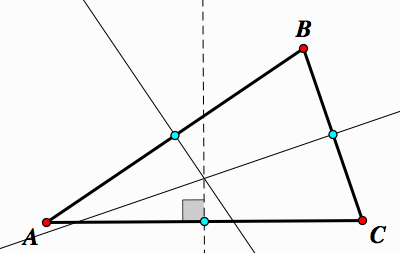
The circumcenter is the point where three perpendicular bisectors are concurrent.

Proof: First, take any △ABC. Construct midpoints on each side of △ABC.

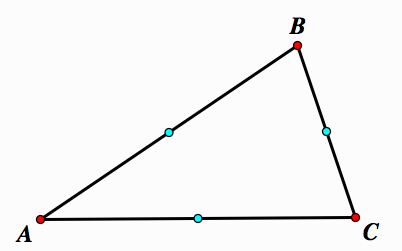
Construct perpendicular lines through each midpoint.

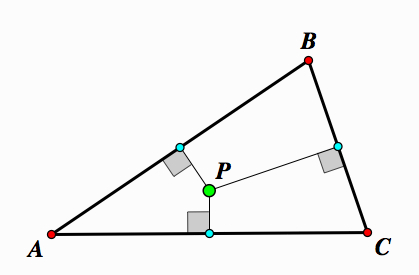Next, construct segments from the vertices of each to the point of concurrency.

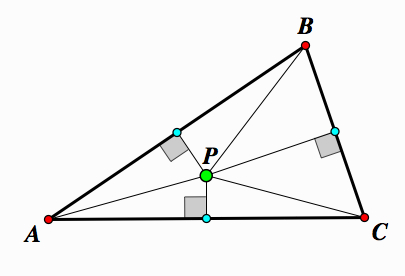
Therefore, we have 3 sets of congruent triangles.

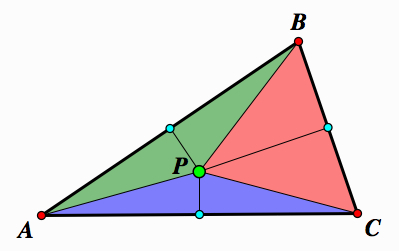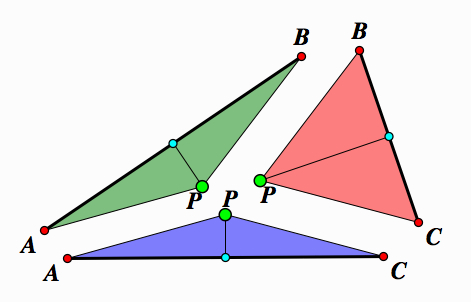So, AP = BP and BP = CP. Therefore, AP = CP. Since each of these are equidistant from the vertices, then they meet at P. Therefore, the perpendicular bisectors are concurrent at point P.

Also, since AP = BP = CP, it follows that A, B, and C are points that lie on a circle. This circle is called the circumcircle of △ABC.

Incenter

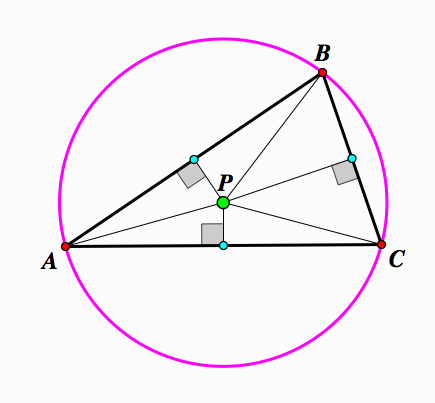
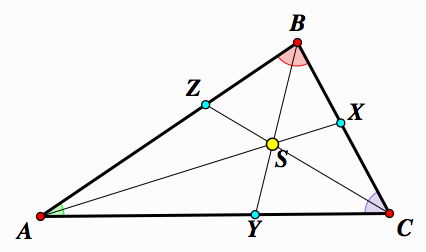
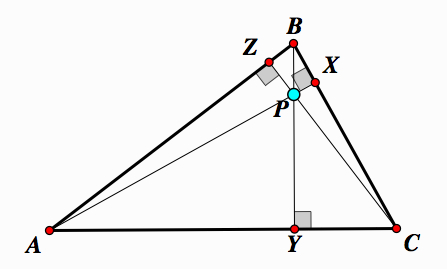
Take any triangle △ABC. The angle bisectors of triangle △ABC are concurrent at one point. This point is equidistant from the sides of the triangle.

Proof: First, take any △ABC.

Construct an angle bisectors at vertex A intersecting BC, at vertex B intersecting AC, and at vertex C intersecting AB.

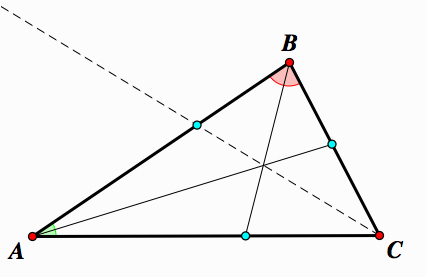This angle bisectors intersect the sides of the △ABC at points X, Y, and Z. We want to prove that these angle bisectors concur at one point.

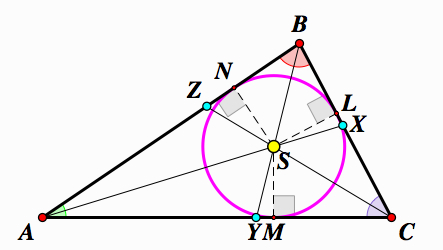
Drop a perpendicular segment from point S to the sides of △ABC. If we look at △ASN and △ASM, we can see apply the AAS postulate. We know∠SAN ≅ ∠SAM , ∠ANS ≅ ∠AMS, and these triangles share the side AS. Therefore, △ASN ≅ △ASM. Similarly, △BXN and △BXL have ∠NBS ≅ ∠LBS , ∠BNS ≅ ∠BLS, and these triangles share the side BS so △BXN ≅ △BXL. Lastly, △CSL and △CSM have ∠LCS ≅ ∠MCS , ∠CLS ≅ ∠CMS, and these triangles share the side CS. Therefore, △CSL ≅ △CSM.

Therefore, we know:

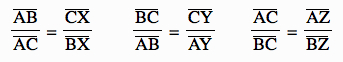
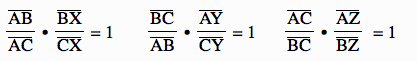
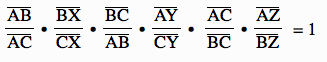
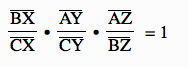
Therefore, by Ceva's Theorem we know that AX, BY, and CZ concur at point S and this point S is equidistant from the sides of triangle △ABC.

Orthocenter

The centroid is the point where the three altitudes of a triangle are concurrent.

Proof: First, take any △ABC.

Construct the altitudes of each side of the triangle.

If you look at △APY and △YPC. We know that:

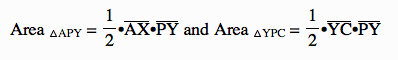
Therefore,

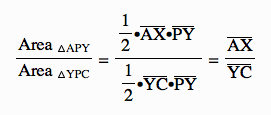
Now, let's look at △APZ and △BPZ. We know that:

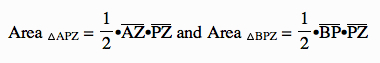
Therefore,

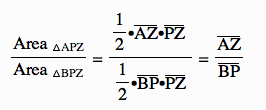
Next, let's look at △BPX and △XPC. We know that:

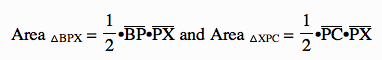
So:

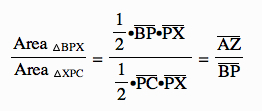
Therefore,

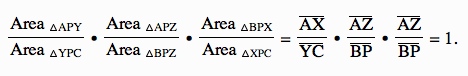
So the altitudes of △ABC are concurrent at a point P.

Blanchet's Theorem

In a triangle △ABC, where AX is the altitude to BC. Construct a line through XZ and through XY. Then AX is the bisector of angle ∠YXZ.

---

 

Desaurges' Theorem

If two triangles are in perspective from a point, then they're also in perspective from a line.

---

 

Menelaus' Theorem

Given a triangle △ABC, and a transversal line that crosses BC, AC and AB at points X, Y, and Z. Then

 

---

Napoleon's Point

Take any triangle △ABC. On the sides BC, CA, AB of the triangle, construct outwardly drawn equilateral triangles. Let the centroids of these triangles be P, Q, and R respectively. Then the lines AQ, BR, and CP are concurrent at Napoleon's Point, point N.

 

---

Van Aubel's Theorem

Let △ABC be a triangle and AX,BY, and CZ concurrent cevians at T. Then:

Proof: First, we construct a △ABC with concurrent cevians.

Look at triangles △AXC and △ABX.

Return to Kate's 6690 Homepage