Primes

When you look at Pascal's Triangle, find the prime numbers that are the first number in the row. That prime number is a divisor of every number in that row.

Powers of 2

Now let's take a look at powers of 2. If you notice, the sum of the numbers is Row 0 is 1 or 2^0. Similiarly, in Row 1, the sum of the numbers is 1+1 = 2 = 2^1. If you will look at each row down to row 15, you will see that this is true. In fact, if Pascal's triangle was expanded further past Row 15, you would see that the sum of the numbers of any nth row would equal to 2^n

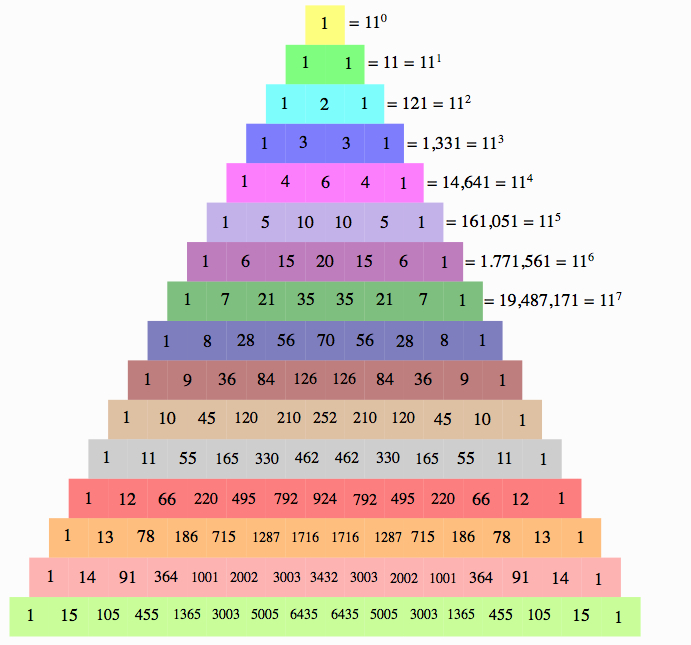
Magic 11's

Each row represent the numbers in the powers of 11 (carrying over the digit if it is not a single number). For example, the numbers in row 4 are 1, 4, 6, 4, and 1 and 11^4 is equal to 14,641. Look at row 5. The numbers in row 5 are 1, 5, 10, 10, 5, and 1. Since 10 has two digits, you have to carry over, so you would get 161,051 which is equal to 11^5.

Hockey Stick Pattern

Start with any number in Pascal's Triangle and proceed down the diagonal. Then change the direction in the diagonal for the last number. That last number is the sum of every other number in the diagonal.

Triangular Numbers

If you start with row 2 and start with 1, the diagonal contains the triangular numbers.

Square Numbers

Down the diagonal, as pictured to the right, are the square numbers. You can find them by summing 2 numbers together. This can be done by starting with 0+1=1=1^2 (in figure 1), then 1+3=4=2^2 (figure 2), 3+6 = 9=3^2 (in figure 1), and so on.

*Note that these are represented in 2 figures to make it easy to see the 2 numbers that are being summed.

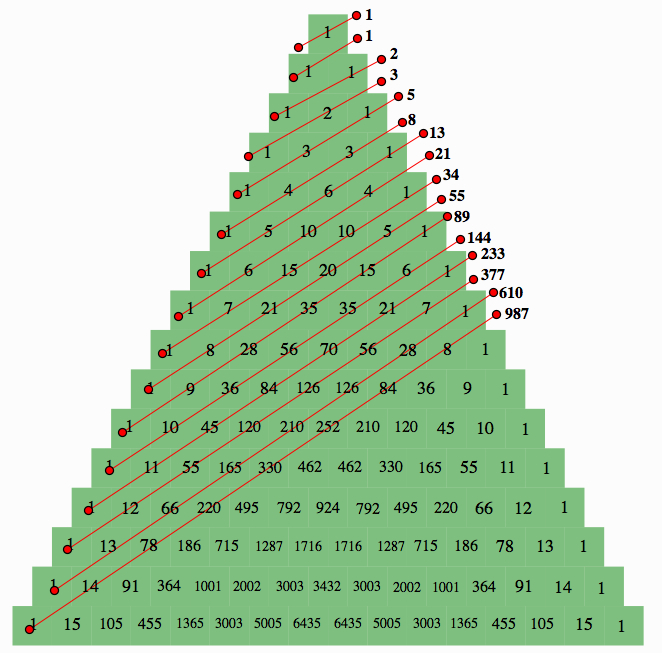
Fibonacci's Sequence

If you take the sum of the shallow diagonal, you will get the Fibonacci numbers.

Catalan Numbers

Catalan numbers are found by taking polygons, and finding how many ways they can be partitianed into triangles. These numbers are found in Pascal's triangle by starting in the 3 row of Pascal's triangle down the middle and subtracting the number adjacent to it.

Binomial Expansion

When expanding a bionomial equation, the coeffiecents can be found in Pascal's triangle. For example, if you are expanding (x+y)^8, you would look at the 8th row to know that these digits are the coeffiencts of your answer. This is true for (x+y)^n.

Fractal

If you shade all the even numbers, you will get a fractal. This is also the recursive of Sierpinski's Triangle.