

Kate Berryman
cavaleri@uga.edu
*Please make sure your browser is maxiumized to view this write up;
In this write up we will investigate parametric equations.
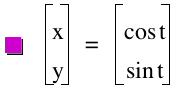
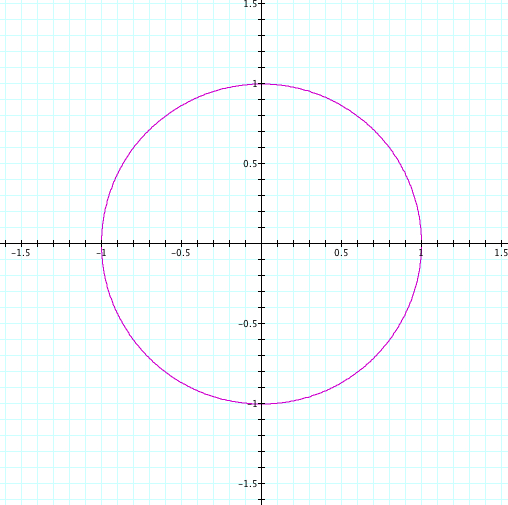
We see with the most basic example that the graph is just a circle with radius at 1. Let's explore further.
Consider:
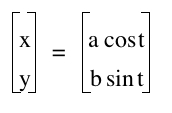
What will happen when we change the values of a and b so that they are not equal to 1? Just for now, let continue to let a=b. Let's look at when a=b=3.
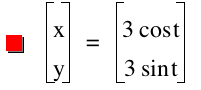
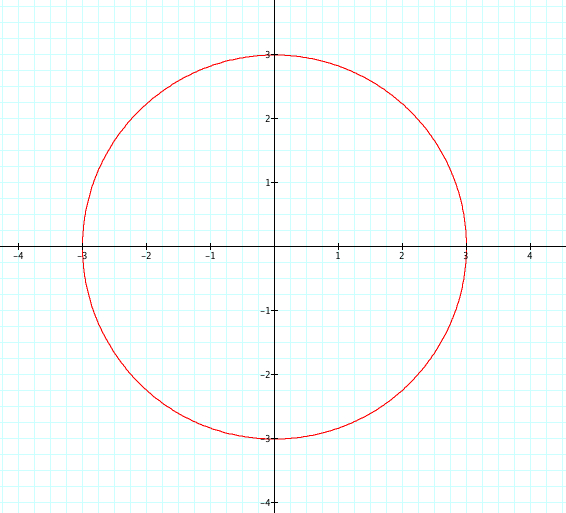
Again, we get a circle. This time with radius 3. It seems fair to assume that the radius of the circle is based on the value of a=b. Let's look at a=b=5 and see if the radius of the circle graph is 5.
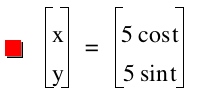
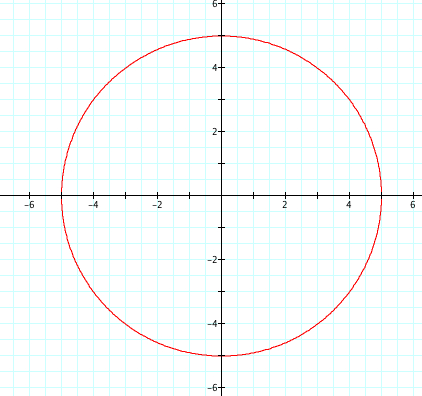
Yes! The radius is 5!
What will happen when a is not equal to b? Let's start by looking at when a>b. We will set a=5 and vary b from 1 to 4, therefore a>b.
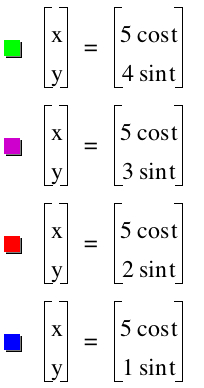
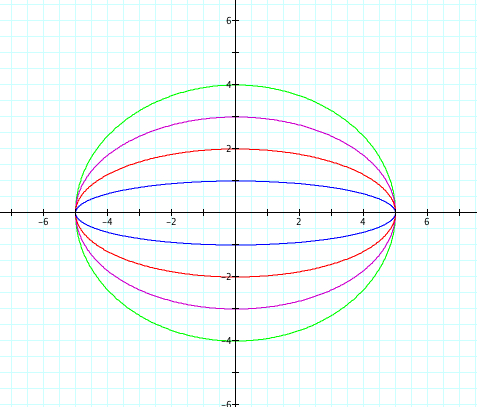
The graphs are all elipses! We can see as the value of b gets smaller and smaller, that the ellipse gets lengthened along the y axis. Notice that the value of a is set at 5 and the length of our elipse passes through 5 and -5. While the width of our ellipse passes through the value of a.
Now, let's compare when a<b. This time we will set b=5 and vary a from 1 to 4, keeping a<b.
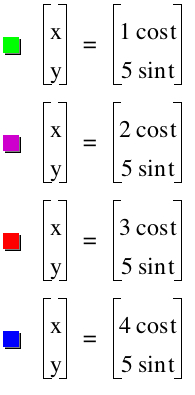
Again, every graph is an elipse, this time widing on the x axis. As values of a change, where the elipse crosses the x axis changes based on the value of a. Meanwhile, the elipse crosses the y axis at the value of b.
As we varied the values of a and b, it will also be interesting to see what happens when we use exponents. Consider:
x=acost^2
y=bsint^2
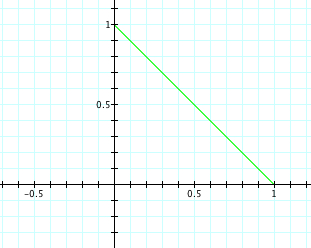
We get a line segment from (1,0) to (0,1). Not very exciting. Let's see what happens though if we change the values of a and b.
Let's see what happens though if we change the value of a=b.
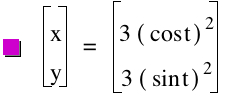
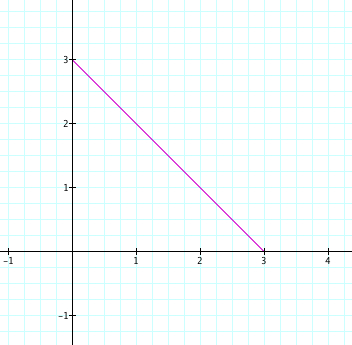
Again, we get a line segment, this time from (3,0) to (0,3). It seems as if the values of a and b affect where this line segment hits the x and y axis. Let's explore this when a does not equal b and see what happens. Let's take a=1 and b=3.
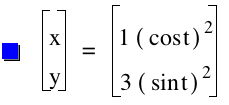
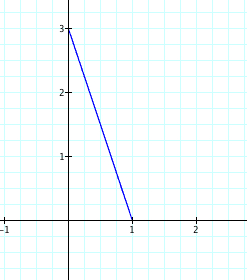
Interestingly, we see that this line segment is connecting the points (3,0) and (0,1). One might conclude that the value of a is where this line segment will connect on the x axis and the value of b on the y axis. Let's look at a=3 and b=1 to see if this assumption is correct.
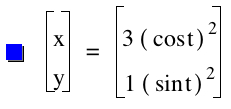
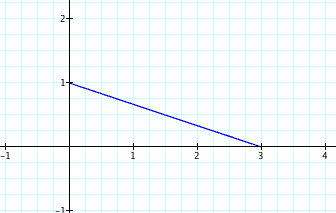
This looks to be the case! We set our a=3 and the line connects with the x axis at (3,0) and we set b=1 and the line touches the y axis at (0,1).
Let's test our idea as our exponent increases.Consider the power of 3, where a=1 and b=3.
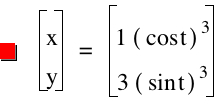
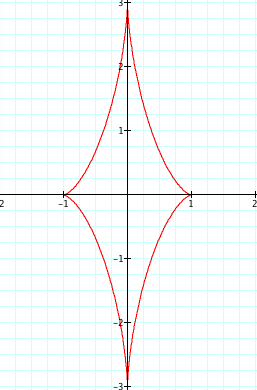
Again, our values of a and b affect where the graph crosses the axis, but now we see more than a line segment. We see a diamond shape with a slight curve. The shape connects with the x axis at our value of a and the y axis at our value of b. Is it safe to assume if we switch the values of a and b, then we will get the same diamond shape, only crossing at (3,0), (0,1), (-3,0), and (0,-1)? Let's see:
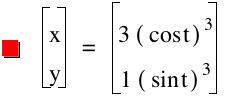
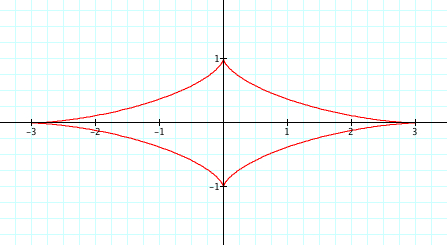
Yes, it is clear again the values of a and b affect the points at which the graph touch the x and y axis. Here we have the same shape, only the graph crosses the axises at (3,0), (0,1), (-1,0), and (0,-3).
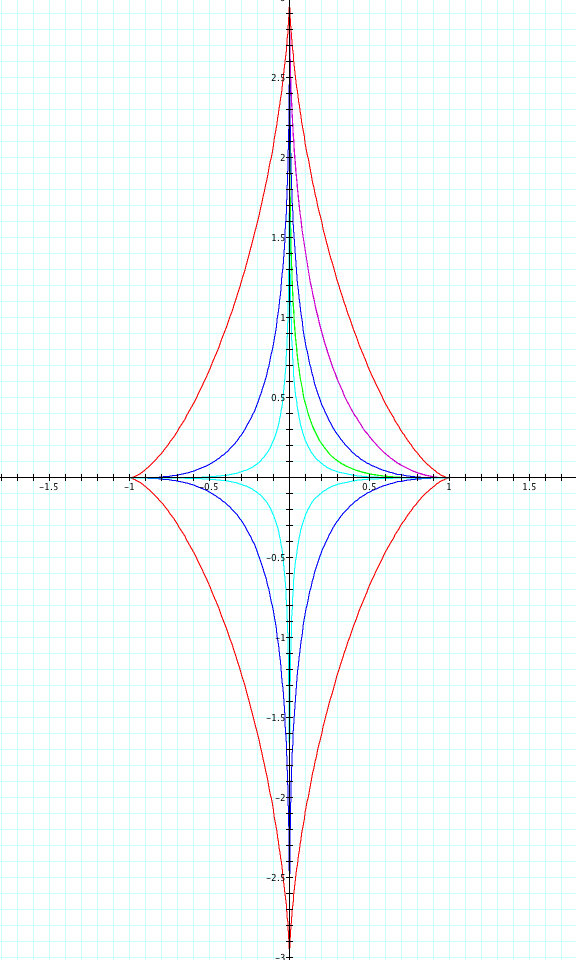
Let's explore with even higher exponential values. First, consider when a=1 and b=3 and take our exponents to be 3 through the 7 power.
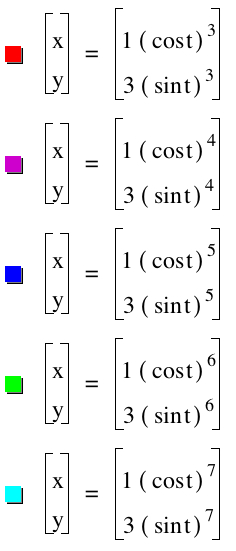 |
 |
Now consider when a=3 and b=1 and take our exponents to be 3 through the 7 power.
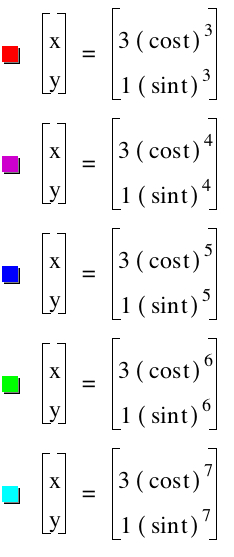 |
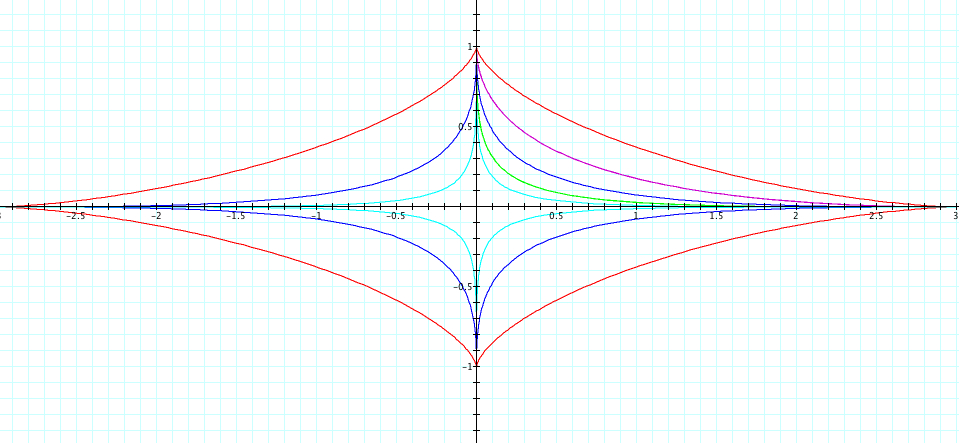 |
We can see as the exponent value increases, the curve is more pronounced. Again, our suspition of why the graphs cross the axis holds true based on the values of a and b. Therefore, when a>b, the graph will be elongated along the x axis and when a<b, the graph will be elongated along the y axis. Yet, if we look closely, we notice something interesting. We see that for even exponents, the graph remains in Quadrant I, while with odd powers, the graph is in all four Quadrants.
Further explorations may look into when sin and cosine are negative or positive. Also, adding and subtracting integers from each equation. There are many more discoveries to be made!!