

Kate Berryman
cavaleri@uga.edu
*Please make sure your browser is maxiumized to view this write up;
In this exploration we will explore the use of spreadsheets in mathematics. We are given the problem about measurements of guitar frets.
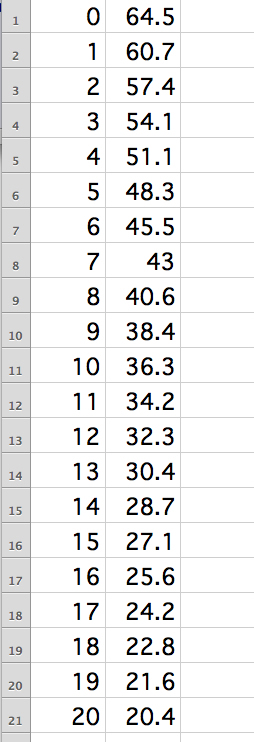
The set of data is formed by measuring the length of a guitar string from a fret to the bridge of the guitar. The open string can be thought of as "fret 0", and the length of the open string is the initial measurement. Then make measures for frets 1, 2, . . ., 20 and plot a graph of the points where the fret number is the x coordinate and the length is the y coordinate.
Below we have the set of data for a guitar measurements from fret to bridge.
Let's look at a graph:
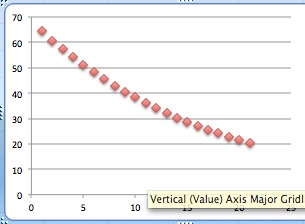
It is some what linear but has a slight curve. Now we will investigate the difference in the first two columns. So we will take B2/B1 and place them in C2. Then drag down from C2 to C23. Here we see the difference in length of each fret.
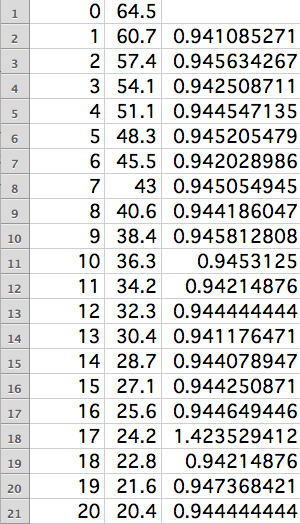
We can see that the ratios are close to being the same, which we would conclude this is close to a linear function. To estimate a better common ratio, let's take the arithmetic mean of the entries in Column C.
![]()
Now let's look to find a function to generate values for the lengths of the string from Frets 0 - 20 using the the function.
![]()
Let's calculate and compare our data list with the values using the function:
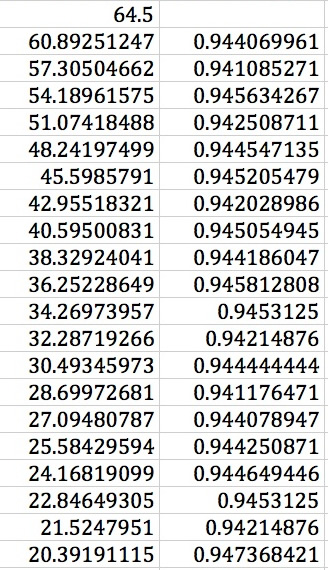
Notice that the result found when using the function is approxiamatly the same as the result found with measured length.
Now let's find the arithmetic mean of the of our function column.
![]()
As we can see this is a much better estimate of the ratio. Therefore this function is the best fit for our set of data.
Further exploration can be done if we use an different instrument with a shorter or longer neck. For example, a bass guitar or mandolin. If the instrument has a shorter neck then there less distance between the fret and bridge. If the instrument is longer, the there distance will be longer from the fret to the bridge.