

Kate Berryman
cavaleri@uga.edu
*Please make sure your browser is maxiumized to view this write up;
The Nine-Point circle for any triangle passes through the three mid-points of the sides, the three feet of the altitudes, and the three mid-points of the segments from the respective vertices to orthocenter.
To start, we begin with some constructions:
Take an arbitrary triangle ABC. |
 |
Take M to be the midpoint of AB, N be the midpoint of BC, and L be the midpoint of AC. |
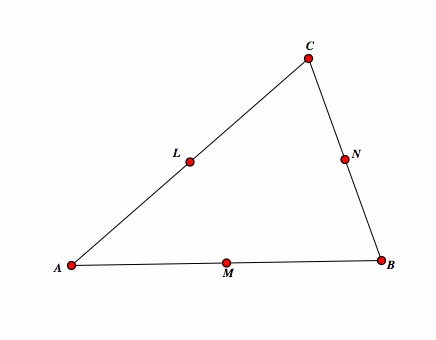 |
Next, take D to be the foot of the height from C to AB, E to be the foot of the height from A to BC, and F to be the foot of the height from B to AC. Here, we see that point O is our orthoceenter. |
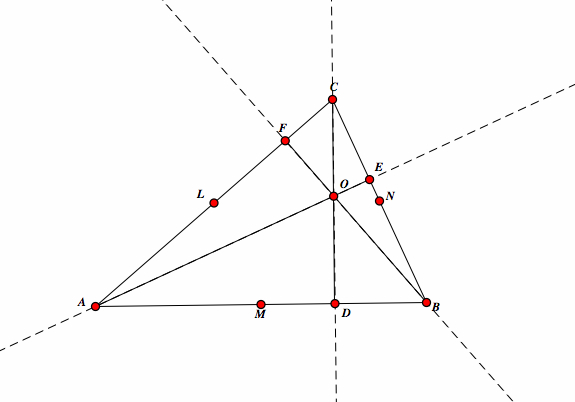 |
Last, take P to be the midpoint of OB, Q be the midpoint of OC, and R to be the midpoint of OA. |
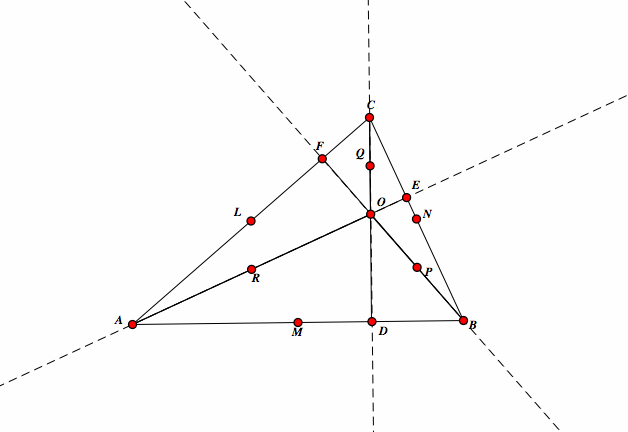 |
How do we prove that points D, E, F, M, N, L, P, Q, and R lie on a circle?
Proof:
| For the first part of this proof, we must remember the theorem that states if a line bisects one side of a triangle and bisects another side of the same triangle, then this line is parallel to the third side of the triangle | |
| Since L bisects AC and N bisects BC, then the line LN is parallel to AB. | 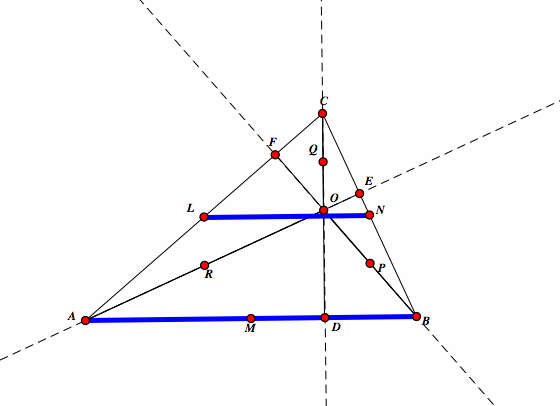 |
| Similiarly, in triangle AOB, R bisects AO and P bisects BO, therefore RP is paralle to AB. | 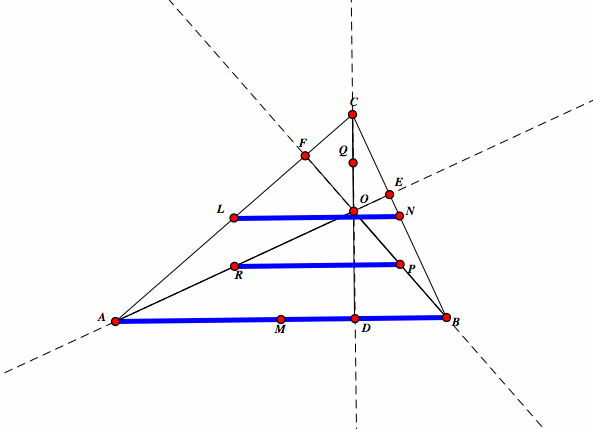 |
| Now, lets look at the right triangle ACD. | 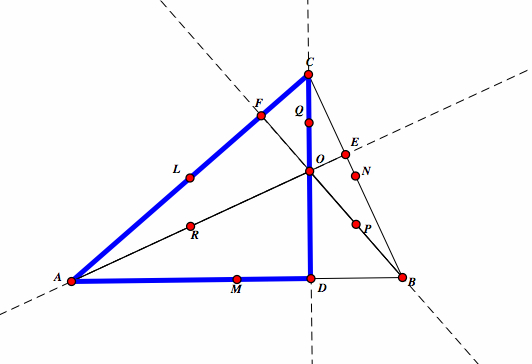 |
| If we drop the foot of the perpendicular on LD to get point T, we see that T bisects AD. Therefore LT is parallel to CD and LR is parallel to CD. | 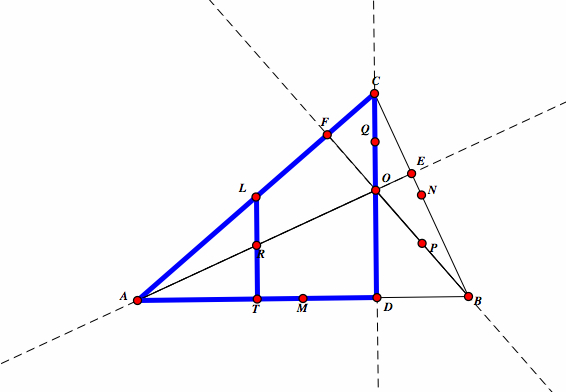 |
| Similiarly, CD is parallel to NP | 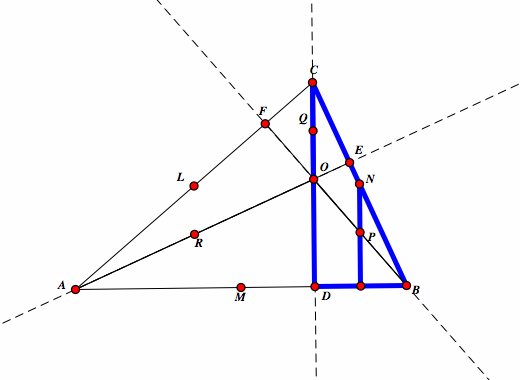 |
| Therefore, NP is parallel to LR. | 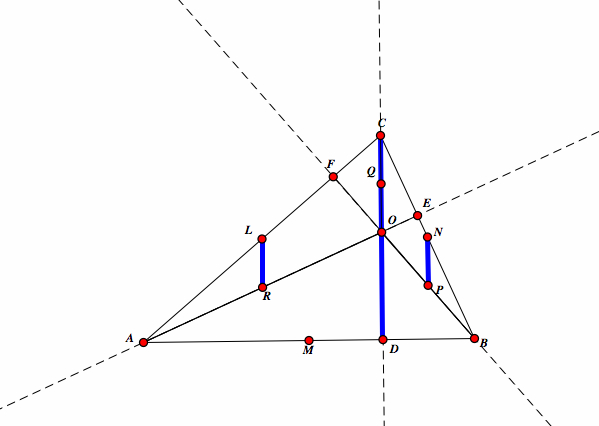 |
| Since LR is parallel to NP and LN is parallel to NP, we have the quadrilateral LNPR, in particular a rectangle with all angles having a measure of 90. | 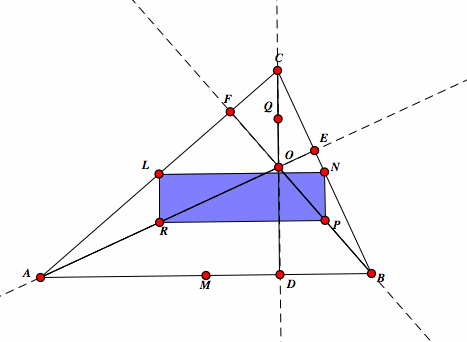 |
| By our previously stated theorem, we have that LM is parallel to BC. | 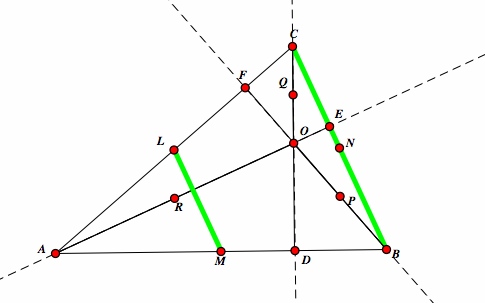 |
| Now lets look at triangle BCO. We know that Q bisects OC and P bisects OB, therefore QP is parallel to BC.It follows that LM is parallel to QP. | 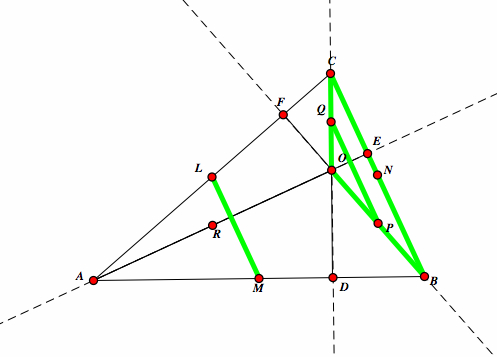 |
| Now, look at triangle AEB. We can see that ABE is a right triangle. Let J be the foot of the perpendicular from M to BE. By our previously stated theorem, MJ is parallel to AE. So, MP is parallel to AE. | 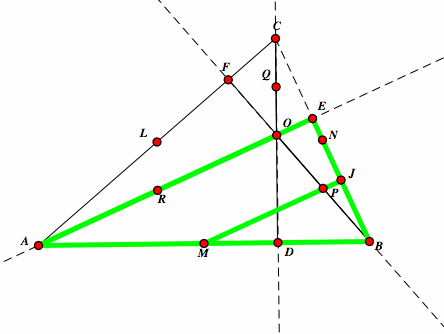 |
| Similiarly, look at right triangle AEC. Let K be the foot of the perpendicular dropped from L to CE. Then, LK is parallel to AE. So, LQ is parallel to AE. |  |
| Since LM is parallel to QP and LQ is parallel to MP, then LMQP is a parallelogram, in particular LMQP is a rectangle since each angle has a measure of 90. | 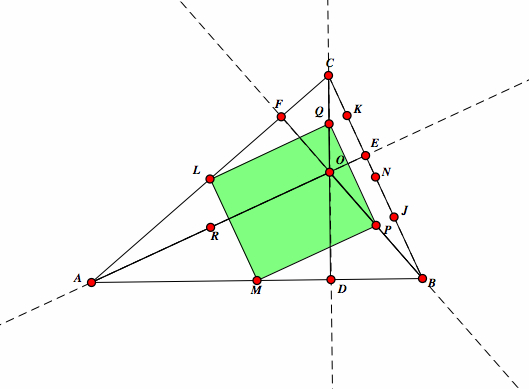 |
| Now, we see two rectangles in our triangle ABC. | 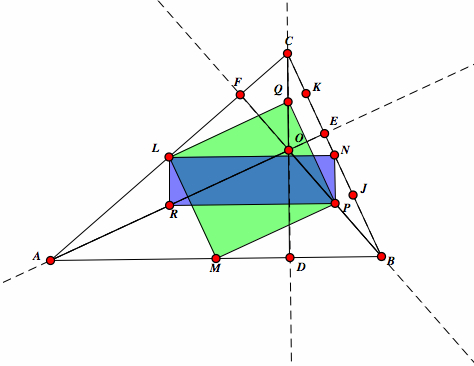 |
| Since LNPR is rectangle, the diagonals LP and NR bisect and are congruent. So LP = NR and they intersect at G. Therefore, LG = PG = NG = RG. | 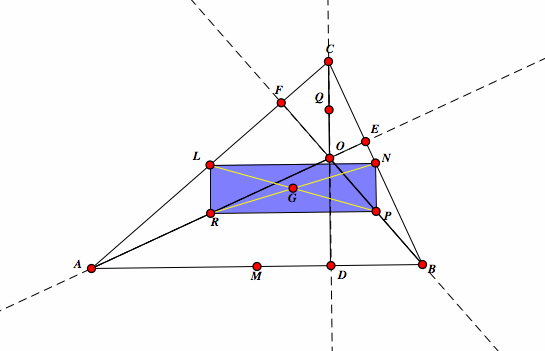 |
| Similiarly, in rectangle LQMP has diagonals LP and MQ that bisect at H. Since LQMP is a rectangle LP = MQ and LH = PH = MH = QH. | 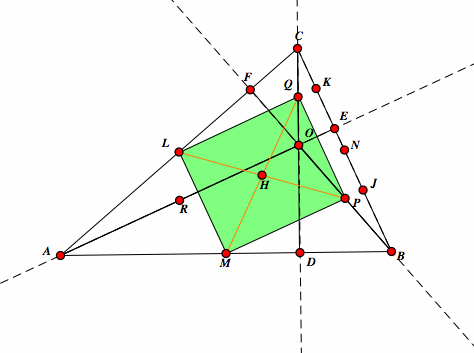 |
| Since LP= NR and LP = MQ then NR = MQ. They intersect G and H in LNPR, so G = H. |  |
| Since LQPM and LNPR are rectangles, so it follows that LG = PG = NG = RG and LH = PH = MH = QH. Since G = H, then LG = PG = MG = QG. So, LG = PG = NG = RG = MG = QG. By definition of a circle, these are six radii with G being the center and L, P, N, R, M, and Q being points the circle. | 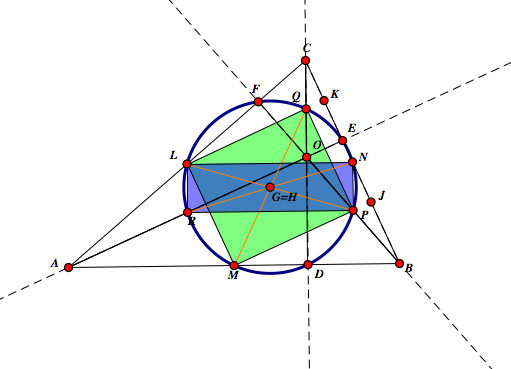 |
| Take the right triangle DQM, with D being the foot of the perpendicular. We see the side QM = QG + GM. We also know that GQ = GM with G as the midpoint. We know by the previously stated theorem that if G is a midpoint of the hypotenuse of right triangle DQM, the G is equidistance from the vertices D, Q, M and a circle passing through D, Q, M has G as its circumcenter. Therefore, D is on the perimeter of the circle. | 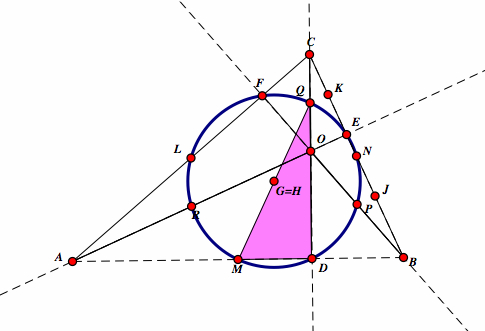 |
| In the same way, lets look at the right triangle LFP. We know that LP = LG + GP and LG = GP. By the previously stated theorem, G is the circumcenter of our circle that has points L, F, P on the perimeter. Therefore, this shows that F is on the perimeter. | 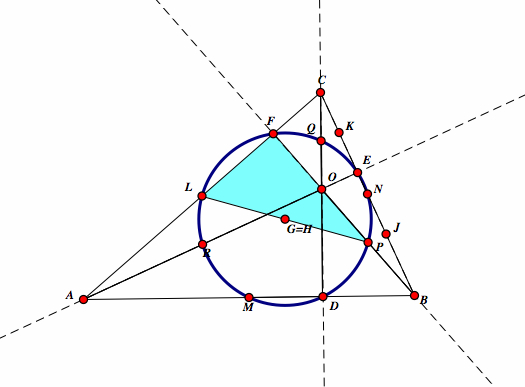 |
| Similiarly, let's look at the right triangle NER, where NR = NG + GR and we know that NG = GR. By our theorem, G again is the circumcenter with points N, E, R on its perimeter giving us our ninth point E. | 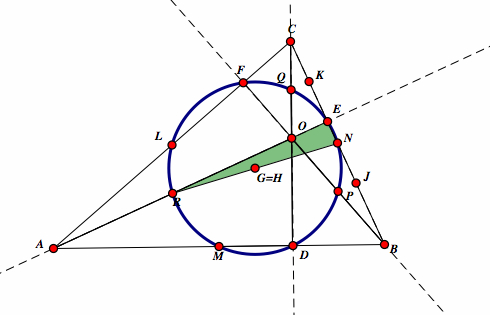 |
| Therefore, G is the center of a nine point circle D, E, F, M, N, L, P, Q, and R. | 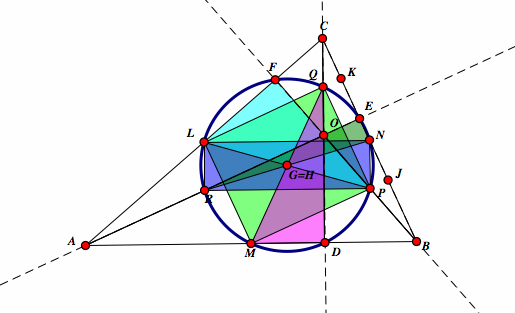 |
| So, we have our nine point circle for our triangle ABC that passes through the three mid-points of the sides, the three feet of the altitudes, and the three mid-points of the segments from the respective vertices to orthocenter. | 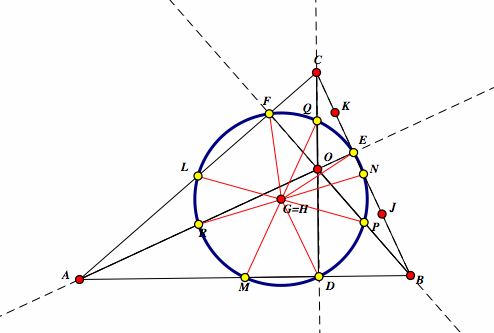 |