Assignment 7

Tangent Circles

Kate Berryman
cavaleri@uga.edu

*Please make sure your browser is maxiumized to view this write up;

In this write up, we will discuss different cases of tangent circles.

First let's look at how to construct a tanget circle.

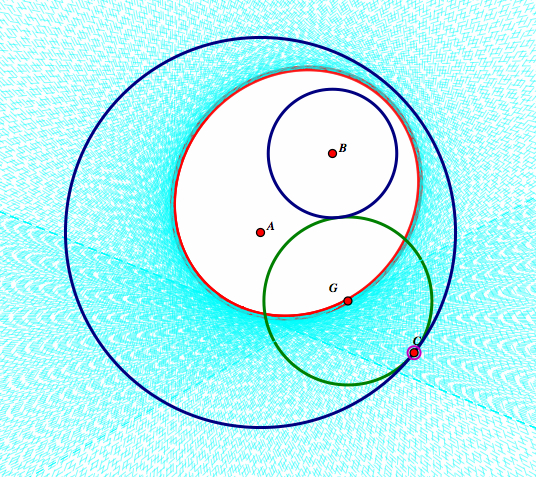
First, construct two circles with center A and center B. (We will look at the case when B is inside of A, however, when completed, B can be moved.) Construct point P to be any point on the circle A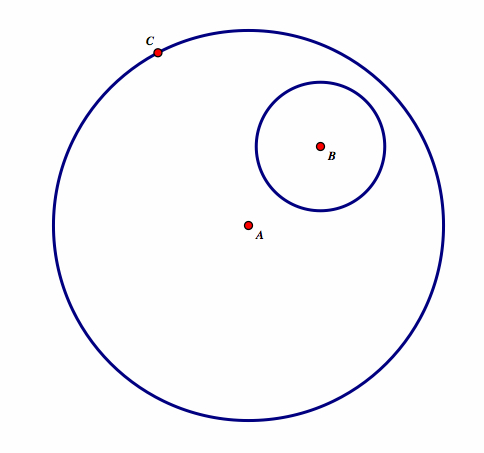
Construct a line passing through AC. Construct a radius on circle B to any point. Let's call this point D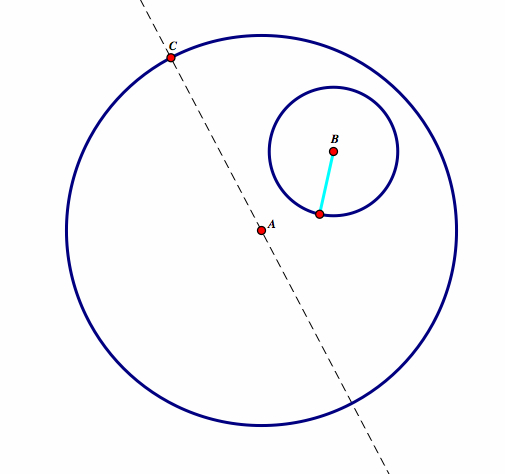
Construct a circle with center C and radius of circle BD. Let's call this point E.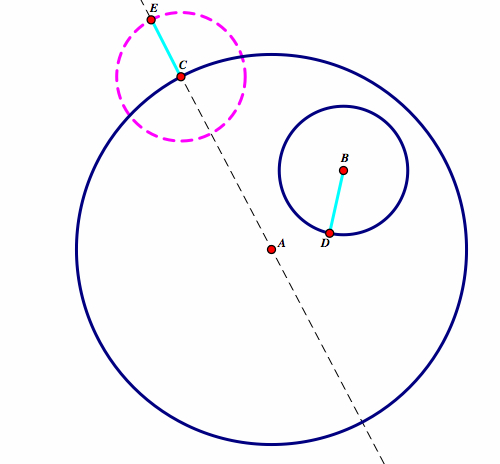
Construct a line segment connecting E and B. Find its midpoint F.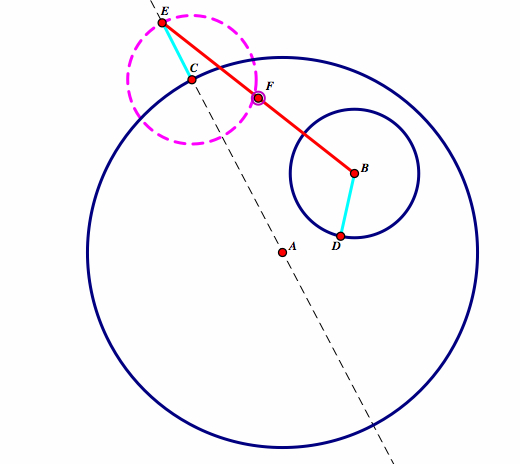
Construct a line that is perpendicular to BE. Where this line intersects line AC, call this point G.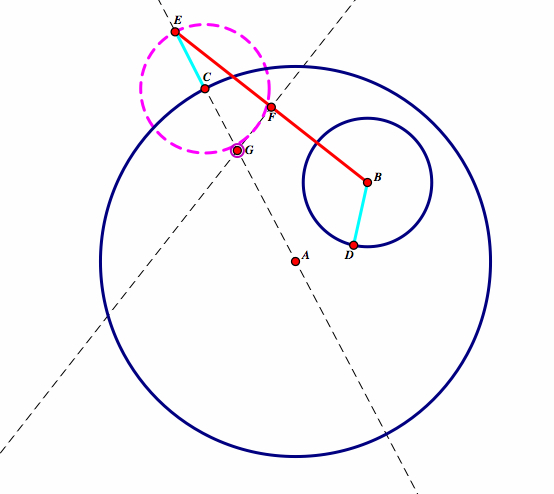
Construct line segments between GE and GB.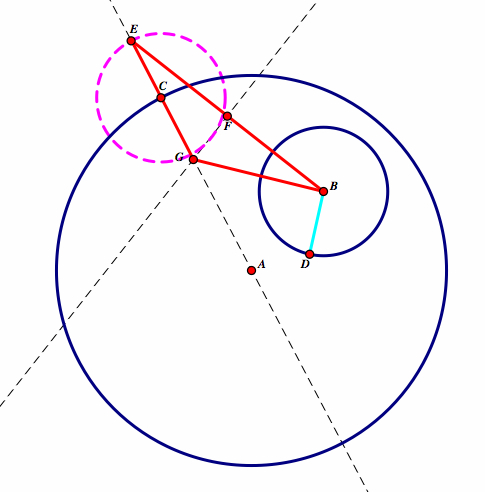
Now, construct a circle with center G and radius of CB.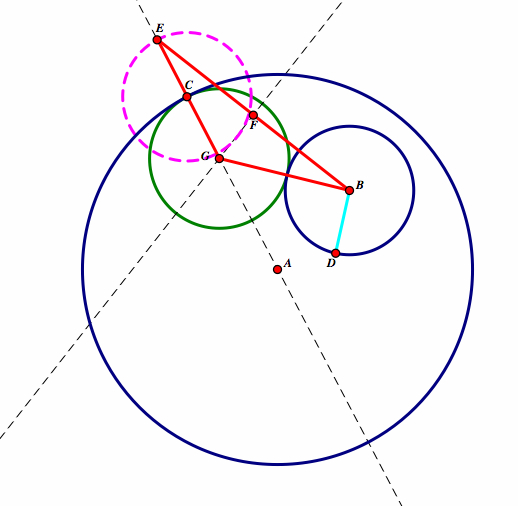
As C moves around circle A, you can see that circle FC is our tangent circle.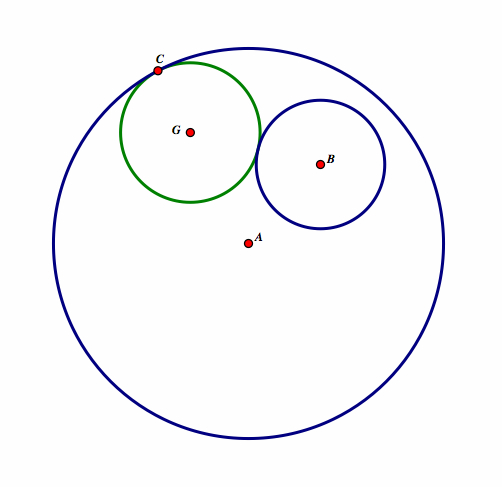
Click Here to have interaction with this tangent circle!!! Move C around the circle A and see what happens! Click Here to see what happens when circle with center A and circle with center B are disjoint! You can also see what happens when circle with center A intersects circle with center B! You can also look in Assignment #5 for the script tools.

Exploration #1
When Circle B is Inside Circle A

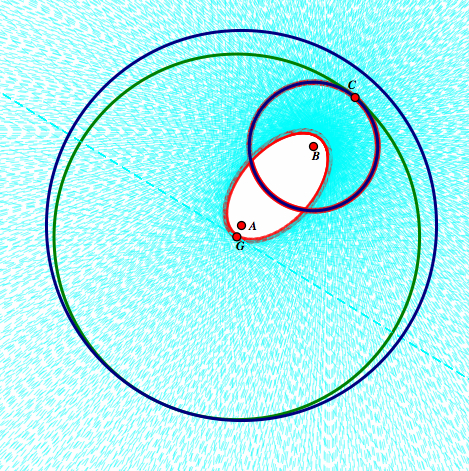
As in our construction, we see the example of when our Circle B is completely contained in Circle A. What happens when we animated our point C and trace our point G?

We see that this gives us an ellipse. Let's remind ourselves what an ellipse is. To be an ellipse, the two focii, in our case points A and B, and their distance to G must be a positive constant.

Let's look back at our construction.

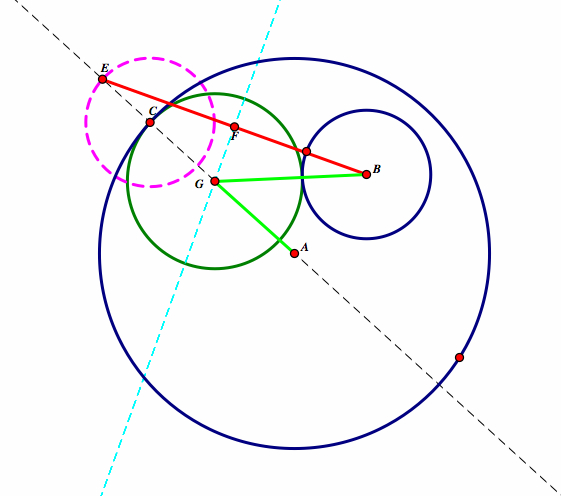
In order to prove this is an ellipse, we must show that AG+BG=a postive contant no matter where C is on circle A. Since line GF is perpendicular to the midpoint of BE, then BG=EG. We also know that AE is equal to the length of the radius of circle B and circle A. Therefore:

AE = AG + GE = AG + BG

So no mattter where C is on circle A, we know that AG+BG is always a positive constant, so this is an ellipse with focii A and B.

Exploration #2
When Circle B and Circle A Intersect

As in Exploration #1, let's trace point G and see what happens as C moves around the perimeter of A.

Again, we see what appears to be an ellipse. Let's look at our original construction to see if we can prove that this is true.

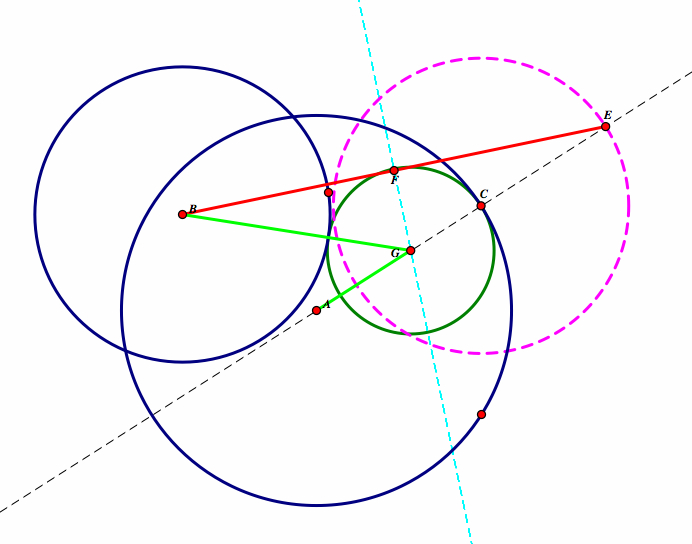
As in Exploration #1, we have that BG = GE and that AE is equal to the radius of circle A and circle B. Therefore, again

AE = AG + GE = AG + BG

So AG + BG will always be a postive constant no matter the point of P on circle C.

Exploration #3
When Circle B is outside of Circle A

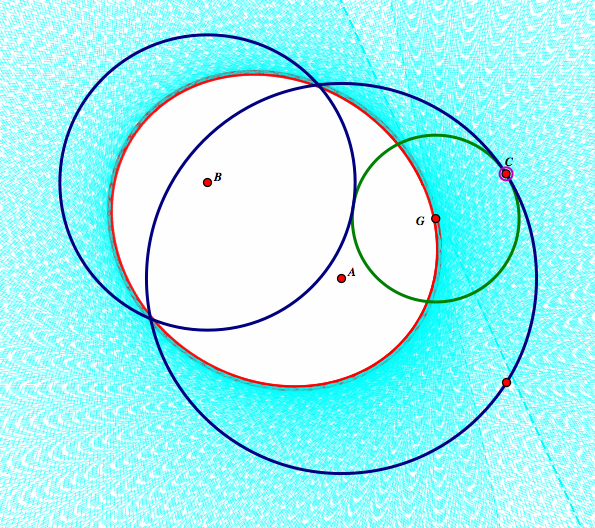
Now, let's animate point C when circle B is outside circle A.

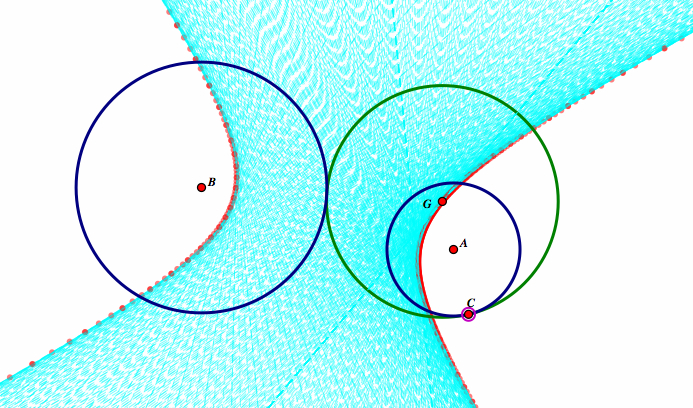
Here we get a very different picture. Instead of an ellipse, we get a hyperbola. We still have to prove that our distance from AG+BG is always a constant positive. Let's look at our original construction.

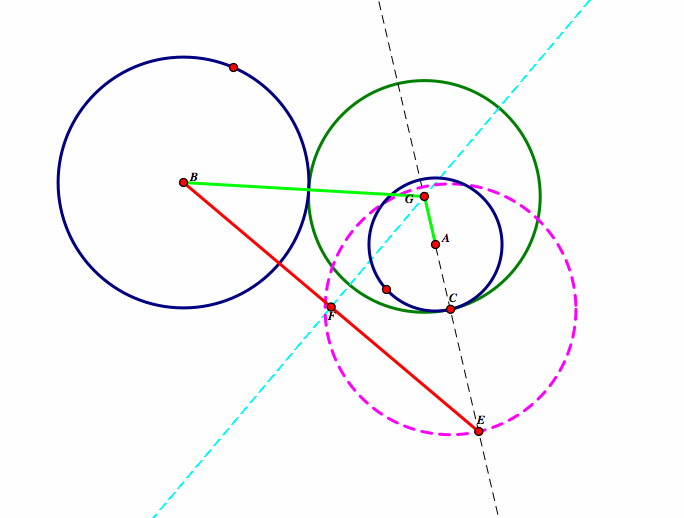
So we know that GB = GE and that GE = GA + AE. Therefore GA = GE - AE or GA = GB - AE. Also, AE = AC + CE. So, we can conclude that AG + BG will always be a postive constant no matter where P is on the perimeter of circle A.

Now we will begin to look at Circle B is constructed inside the Circle G

Exploration #4
When Circle B is inside of Circle A

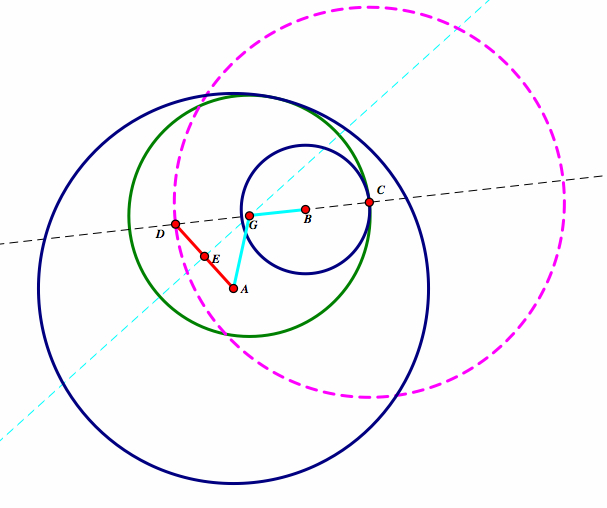
Again, we know that DG = AG. Also, BD = BG +DG. Therefore:

BD = BG + DG = BG + AG.

This again gives us a positive number for AG+BG. So no matter the point on P on circle A, these will remain positive constants. Therefore, A and B are focii of our ellipse.

Exploration #5
When Circle B and Circle A Intersect

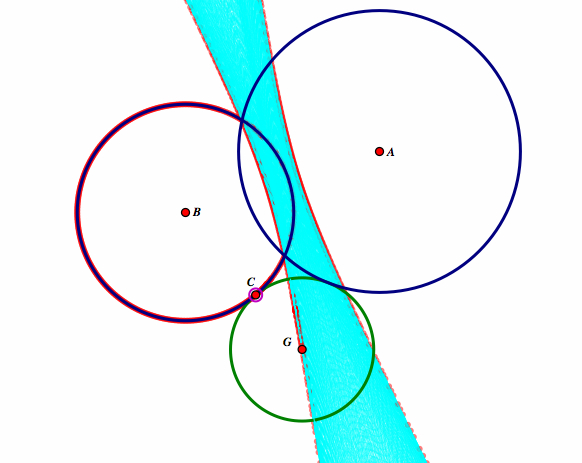
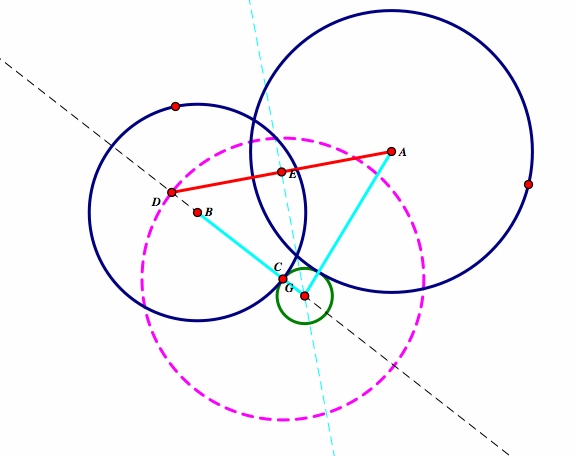
So from construction, AG = DG. Notice that DG = BD-BG or DG = BG + BD. Therefore, again we have the result of:

BD = BG + DG = BG + AG.

Exploration #6
When Circle B is outside of Circle A

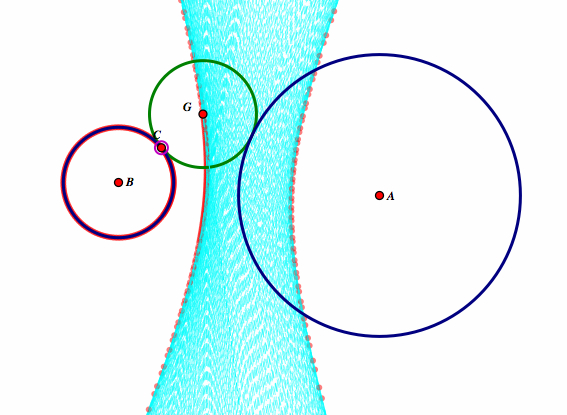
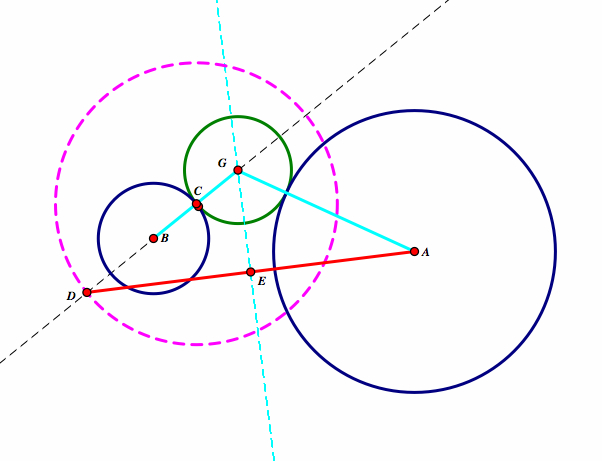
This is also a hyperbola. Again, we have AG=DG. Also, DG - BG = BD or DG = BG + BD. Therefore, again we have the result of:

BD = BG + DG = BG + AG.

To summarize we notice that the loci of the center of the two circles form either a hyperbola or an ellipse. When our circle B was not contained inside the tangent circle, then the trace of the center point of the tangent circle formed a hyperbola. When our circle B was contained or intersected our tangent circle, then the trace of the center point of our tangent circle formed an ellipse. In all explorations, we see that A and B are the focii of either an ellipse or a hyperbola.

Return the Kate's Homepage