

Kate Berryman
cavaleri@uga.edu
*Please make sure your browser is maxiumized to view this write up;
Let's begin with the construction of the pedal triangle.
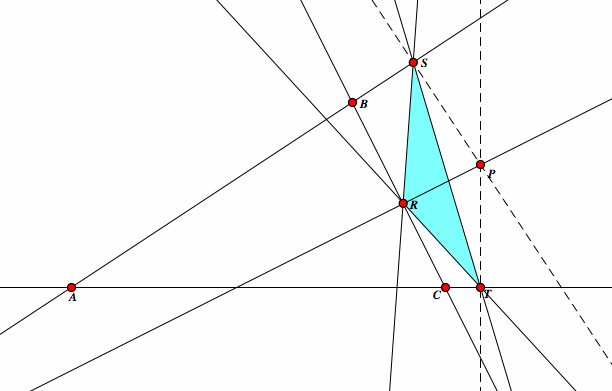
| First, pick three arbitrary points in our plane, say A, B, and C. |
|
| Now, construct lines passing through AB, BC, and AC to get triangle ABC. | 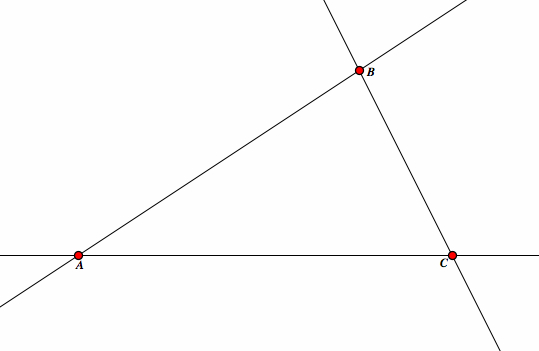 |
| Pick any point P. | 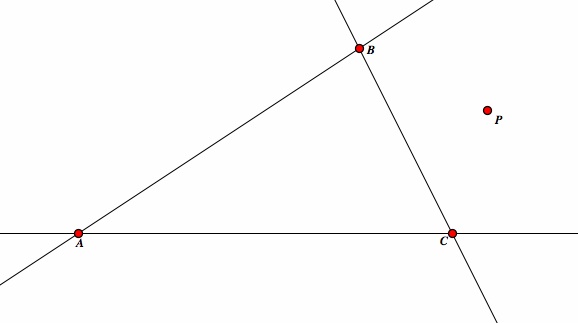 |
Construct a line passing through point P perpendicular to AB, another line passing through point P perpendicular to BC, and another line passing through point P perpendicular to AC. Let's call the intersections of these perpendicular lines R, S, and T respectively. |
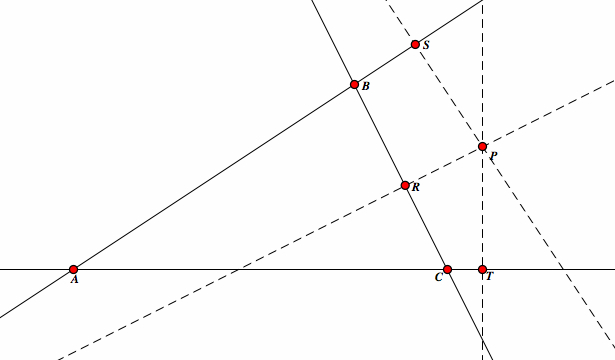 |
| Next, construct a line passing through ST, a line passing through SR, and a line passing through TR. | 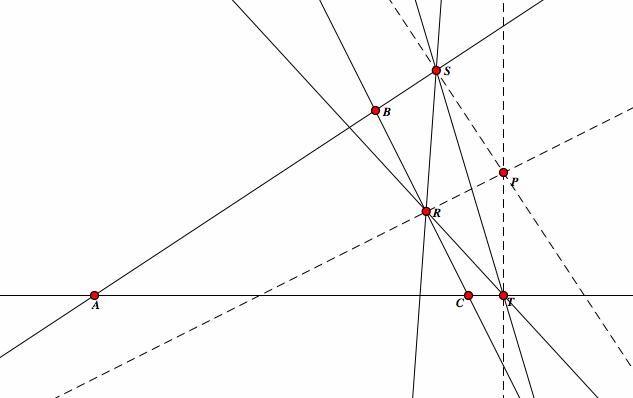 |
The triangle RST is our pedal triangle |
 |
We are going to look at the condition in which a pedal triangle is a degenerate triangle. This is called the Simson Line.
| First, construct a triangle ABC and its circumcircle. Place a point, P, on the circumcircle. | 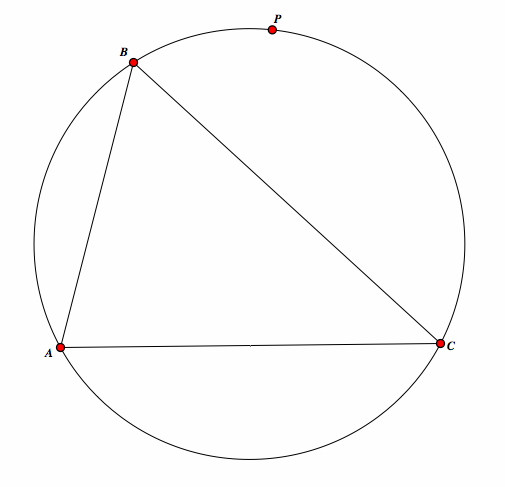 |
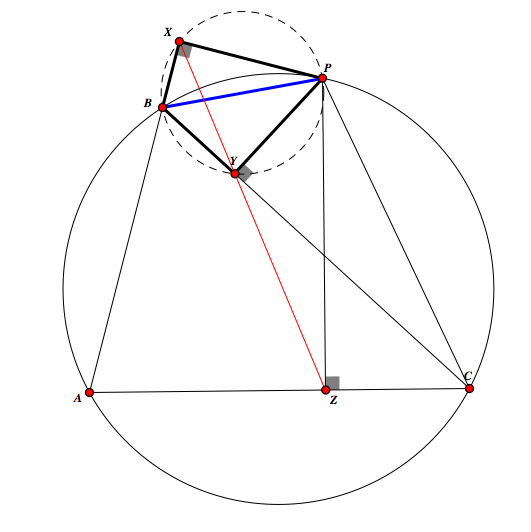
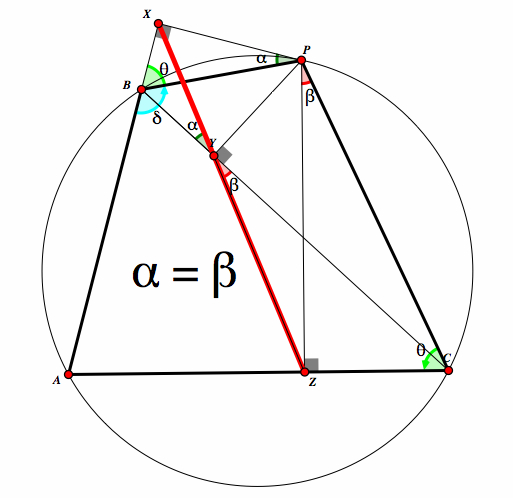
Next, construct perpendicular lines from point P to AB, BC, and AC. Call these points XYZ. Construct segments BP and CP. If we look at the quadraleral BXPY, we see that triangle BXP and BYP are both right triangles that share the hypothenus BP. Therefore, BP is the diameter of a circle and BXPY is cyclic. |
 |
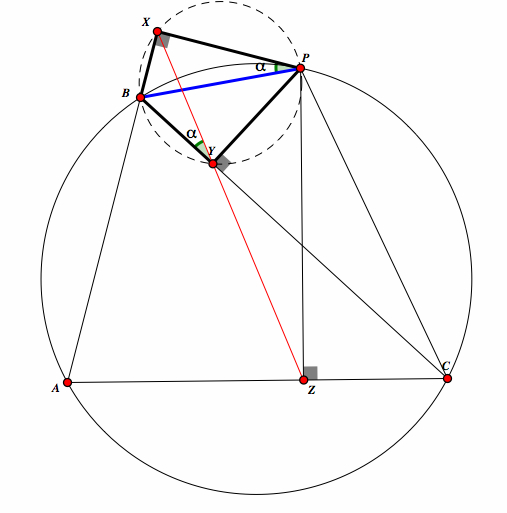
Since angles XPB and XYB are inscribed in the circle and share an arc, then the mearsure of there angles is equal. We will call this α. Also, the since we know the sum of the measure of the triangle BXP is 180 and the measure of BXP is 90, then the angle XBP and α equals 90. |
 |
Notice that triangles PZC and PYC are both right triangles and share the hypothenus CP. Then, CP is the diameter of a circle and YPCZ is cyclic. |
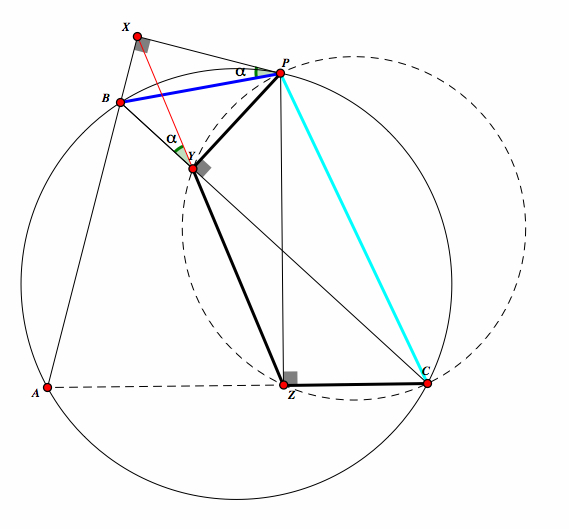 |
Since angles XYC and XPC are inscribed in the circle and share an arc, then the mearsure of there angles is equal. We will call this β. Also, the since we know the sum of the measure of the triangle ZPC is 180 and the measure of CZP is 90, then the angle ZCP and β equals 90. |
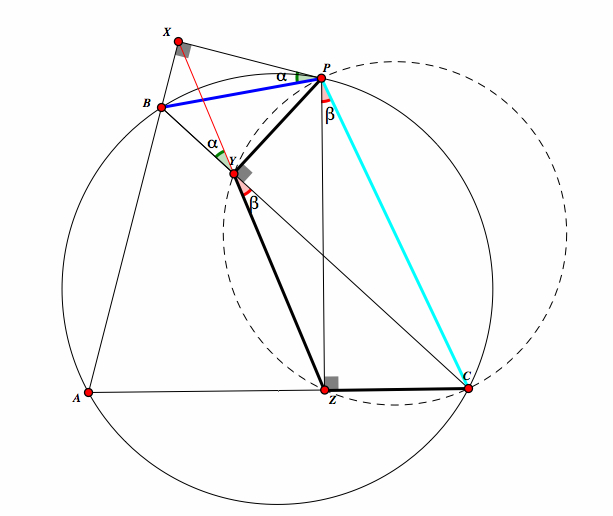 |
| Since P is a point on the circumcircle, then ABPC is a quadrilateral. So we know that and PCA and angle ACP is equal to 180. Lets call these θ and δ. | 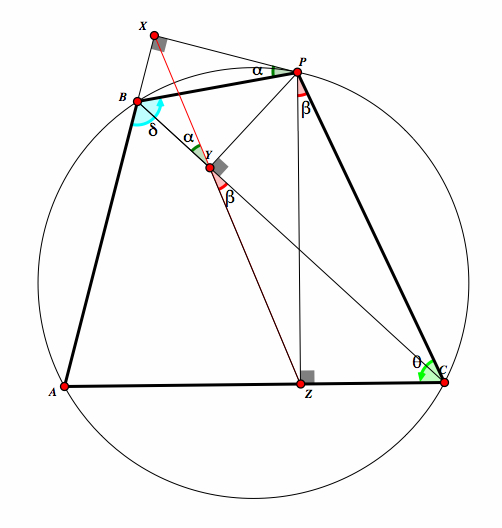 |
| Now we know that θ + δ = 180. But we also know that A, B, and X are colinear, so δ and the measure of the angle PBX is also 180. Therefore PBX is also equal to θ. | 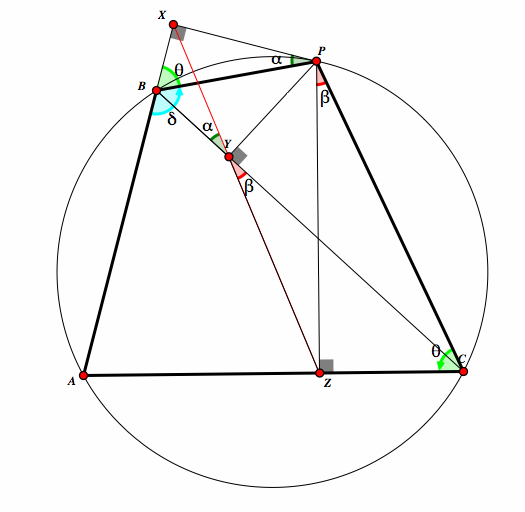 |
Since α + θ = 90 and β + θ = 90, then it follows that α = β. Since α and β are opposite angles then it follows that X, Y, and Z are colinear. This is called the Simson Line. |
 |
This proof done in reverse is the proof to show that the pedal triangle XYZ is degenerate.
Click Here for a JavaScript of a Pedal of a Pedal of a Pedal Triangle!!
Click Here for a Script Tool of a Pedal of a Pedal of a Pedal Triangle!!