

Linear Functions
by Venessa Brown
The goal of this assignment is to explore the sum, product, quotient and composition of two linear functions.
What are linear functions?
Typically, linear functions are defined to be degree-1 polynoimals with one variable. For example, f(x)= x + 6. However there are many forms to express linear functions. This assignment will focus on the slope - intercept form; f(x) = mx + b. Therefore, the above function has slope 1 and y-intercept 6. The graph of a linear function is always a straight line.
f(x) = 6x + 3, g(x) = 7x + 3, and h(x)= (6x + 3) + (7x + 1)
Note: Due to the limitations of graphing calculator, the graphical demonstrations will notate functions as y = instead of f(x), g(x), and
h(x) =
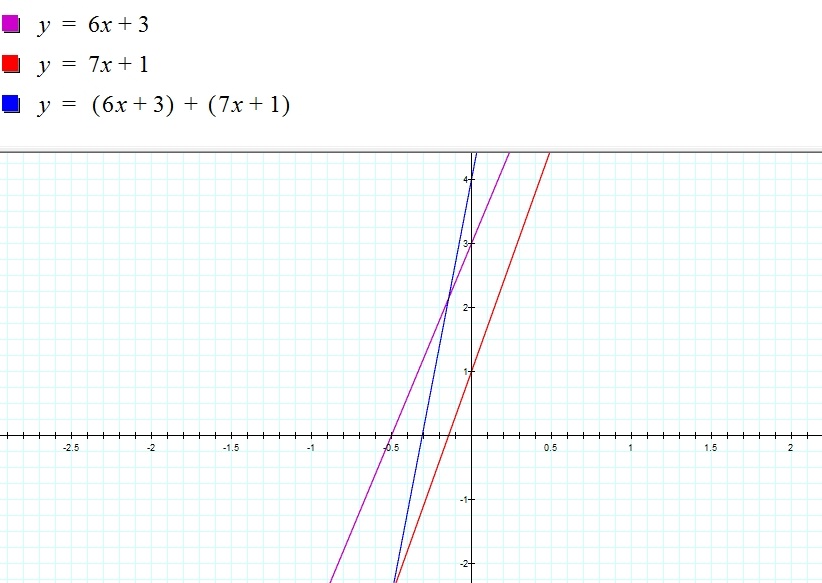
Notice that in the graphical representation above, the summation of the two linear function is also a linear function (the blue line is the result of adding 6x +3 and 7x + 1). Given what we know about algebra, adding first-degree polynomials would include: the process of adding the coeffiecients of the variable together (without changing the degree of the variable) and adding the constantly together; if the functions permit. Example:
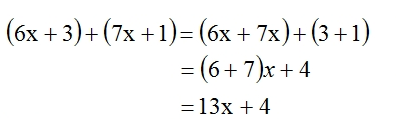
Therefore, the the blue line (the resulting linear function), has slope 13 and y-intercept 4.
Other examples:
1) f(x) = 2x + 1, g(x) = x + 6, and h(x)= (2x + 1) + (x + 6)
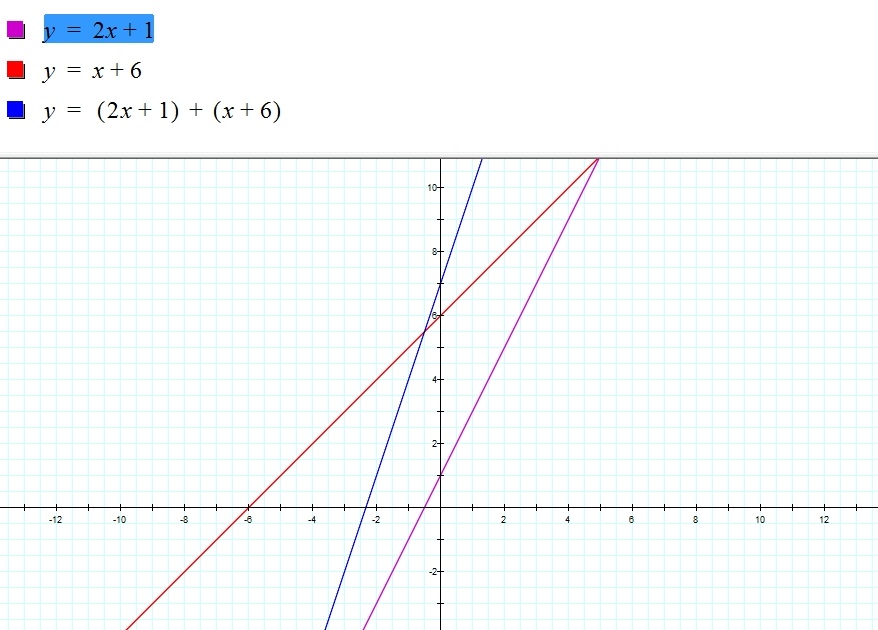
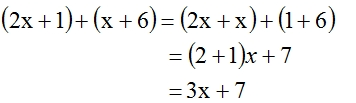
2) f(x) = x + 2, g(x) = x + 7, and h(x)= (x + 2) + (x + 7)
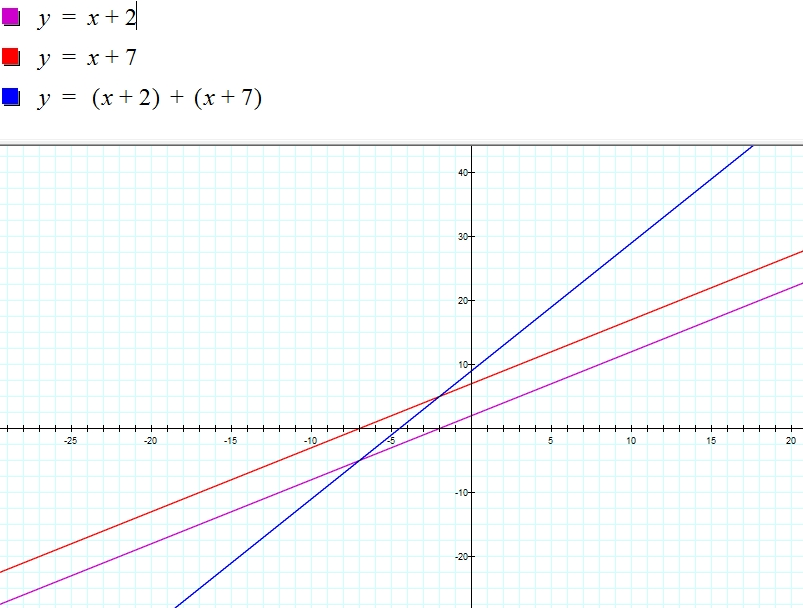
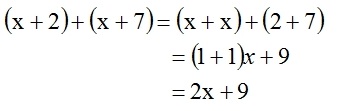
Will the summation of two linear functions always result in another linear function?
General argument
Let a, b, c, and d be any real numbers. Two linear functions can be written as ax + b and cx + d.
Adding:

Multiply linear Functions
f(x) = 2x + 1, g(x) = x + 6, and h(x)= (2x + 1) (x + 6)
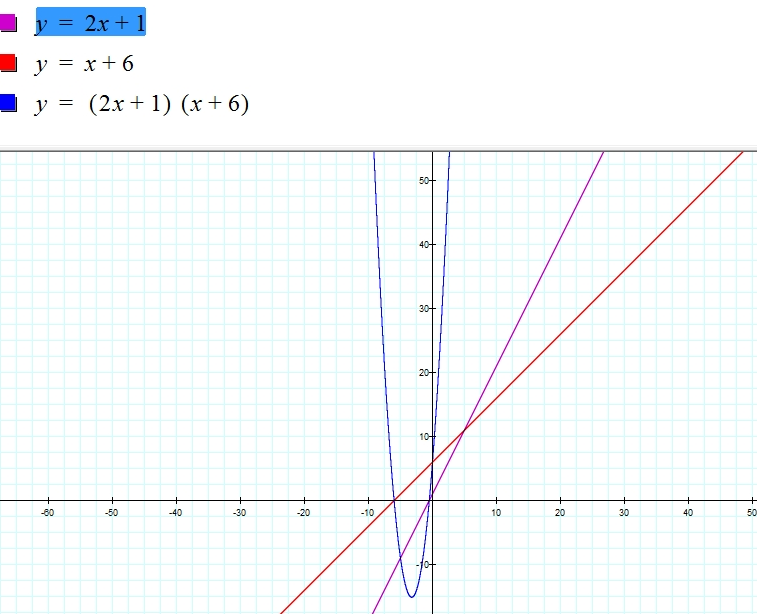
Notice that in the graphical representation above, the product of the two linear function is the graph of a parabola whose fuction is quadratic (degree 2).

Another example:
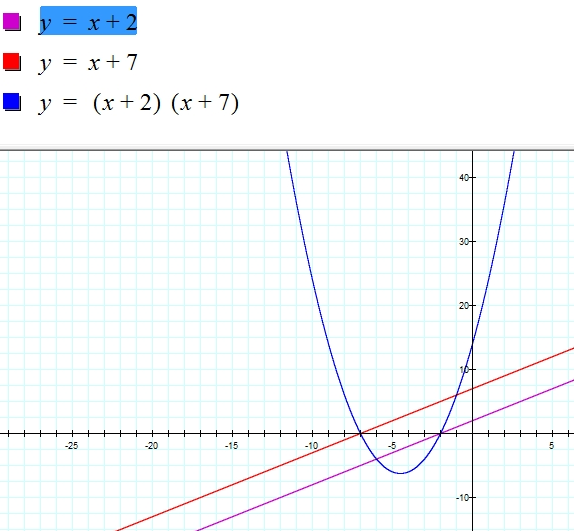
The product does in fact yield a quadratic

Will the product of two linear functions always result in a quadratic function?
General argument
Let a, b, c, and d be any given real numbers. Two linear functions can be written as ax + b and cx + d.
Multiplying:

Further investigations also revealed:
Dividing Two Linear Functions
f(x) = x + 2, g(x) = x + 7, and h(x)= (x + 2) / (x + 7)
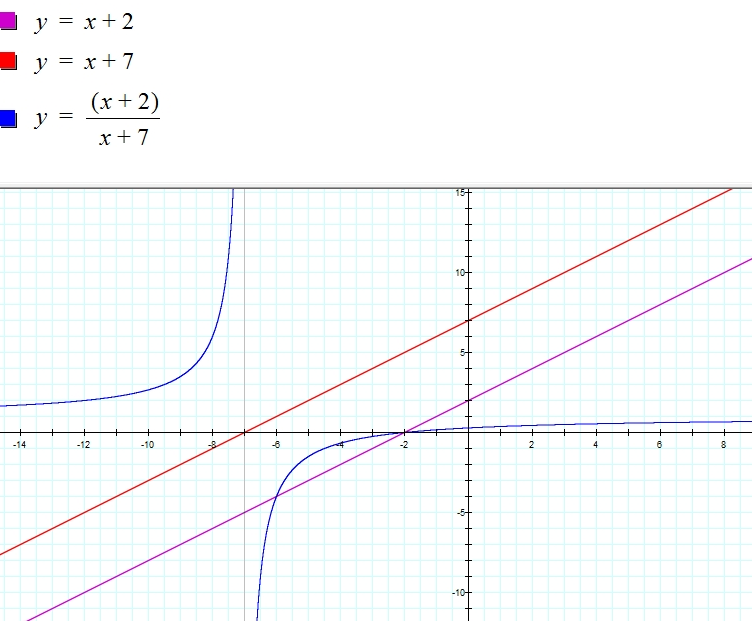
Notice that dividing two linear functions resulted in a graph of a hyperbola.
Important facts about Hyperbolas in the form h(x) = ax+b / cx+d
1. asymptotes intersect at the symmetry of the hyperbola
2. vertical asymptote is the root of cx+d
3. horizontal asymptote is a/c
In the above example, notice that two arms of the hyperbola (so to speak) are approching -7. In fact, -7 is the root of g(x).
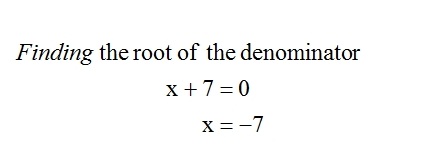
vertical asymptote is -7
Also, the remaining arms of the are approaching 1. This is horizontal asymptote h(x) = a/c = 1.
Another Example:
f(x) = 6x + 3, g(x) = 7x + 1, and h(x)= (x + 2) / (x + 7)
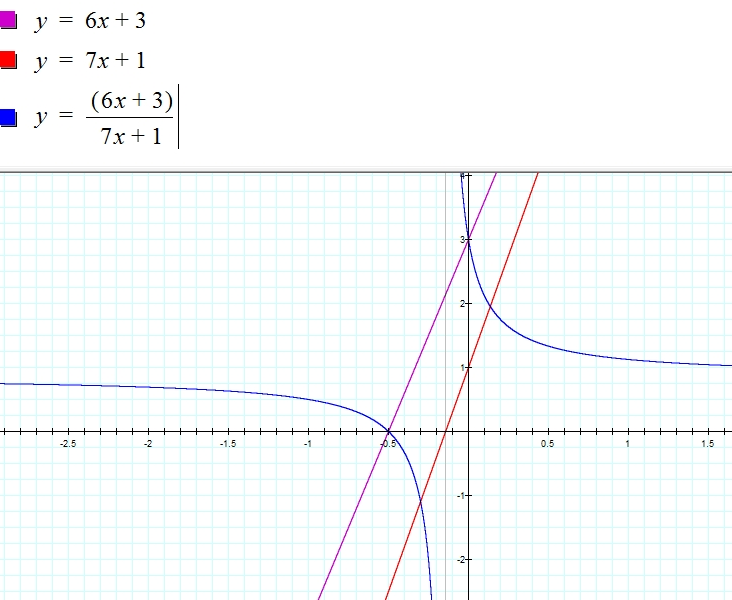
horizontal asymptote h(x) = 6/7
Vertical asymptote x = -1/7
Composition of two linear functions
f(g(x))
f(x) = x + 2, g(x) = x + 7, and f(g(x))= (x + 7) + 2

Notice that in the graphical representation above, the compositon of the two linear function is also a linear function.
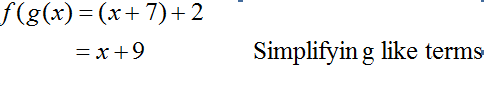
Another example:
f(x) = 6x + 3, g(x) = 7x + 1, and f(g(x))= 6(7x + 1) + 3
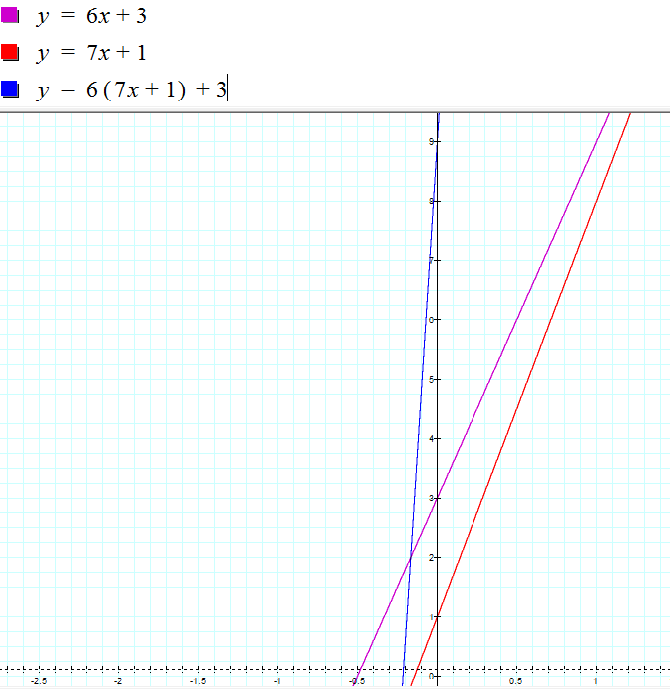
The compostion of this function is also a straight line.

Will the composition of two linear functions always result in a linear function?
General argument
Let a, b, c, and d be any given real numbers. Two linear functions can be written as f(x)= ax + b and g(x) = cx + d.
The compostion f(g(x)) is:
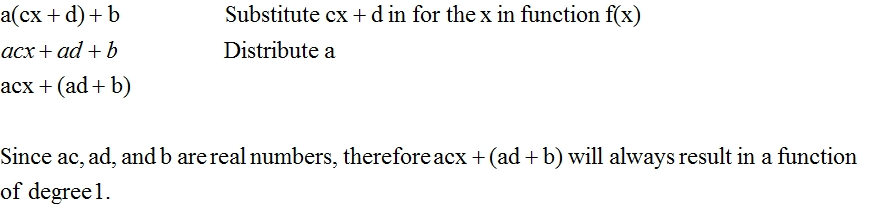
The composition of g(f(x)) is:
Therefore, the compostion of two linear function will always be linear.