

by Venessa Brown
Part One:
Ceva's Theorem
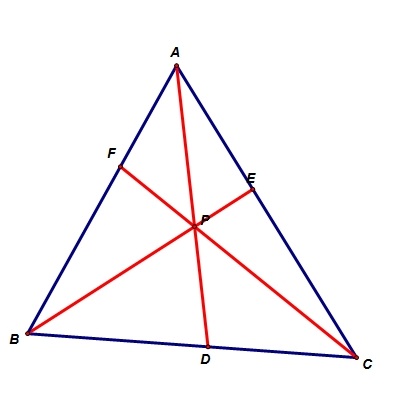
Given a triangle ABC with an arbitrary point P inside the triangle. Any segment from a vertex to the intersection with the opposite side is called a Cevian. Let D, E, and F be the feet of the Cevians opposite A, B,and C respectively.
Prove :
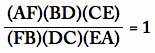
Proof
Consider Area of triangles BDP and CDP.
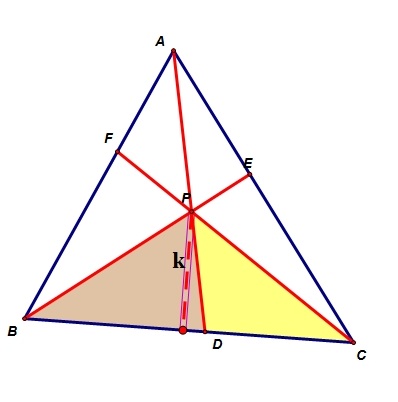
Notice that both triangles are adjacent and share the same altitude k. Computing the ratio of the areas should yield BD/CD.
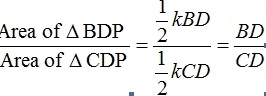
Now consider areas triangles ABD and ACD.
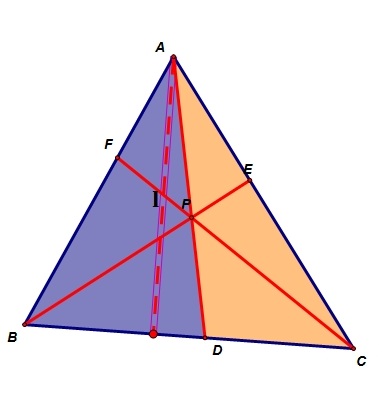
Again, we notice that the two triangles are adjacent and share the same height. Computing the ratio of the areas should yield BD/CD.
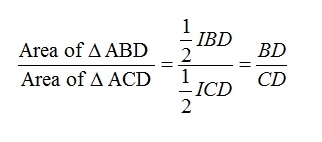
To get to our proof we want to show that:

So the area of Triangle APB can be obtained by subtracting the area of triangle BDP from area triangle ABD. Likewise the area of triangle APC can be obtained by subtracting the area of triangle CDP from area triangle ACD.
Lets evalute the ratio of the areas to confirm what we want to show above.
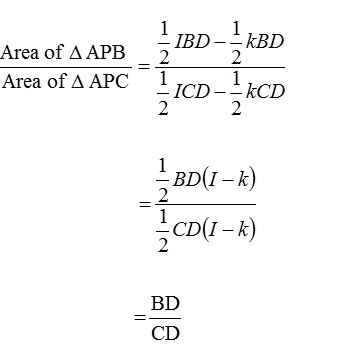
Confirmed
Similar reasoning would show that:

Therefore,

The Converse To Ceva's Theorem
We have already proven that
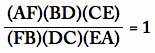
Goal: Show that BE, CF, AD are concurrent.
Proof:
First, we will assume that CF and BE are cevians that intersect at point P. The other cevian that passes through point P is AG.
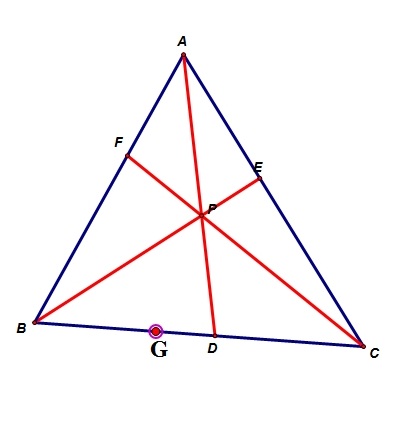
Using Ceva's Theorem, then:
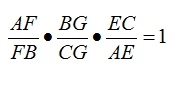
and we have already shown that:
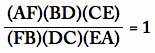
Since these two statements both eqaul 1. We can set up this equality:
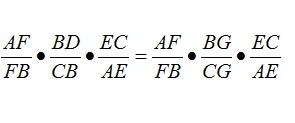
So
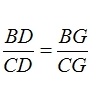
Therefore, D = G.
Meaning that D and G are the same point, proving that BE, AD, CF must be congruent.
Applying the Converse of Ceva's Theorem to Medians of a Triangle
Since medians are constructed by connecting the midpoints of the segments to the opposite vertex. We can then directly apply the converse to Ceva's theorem, to conclude that the meadians are concurrent.
Part Two:
Rhombus construction given one side and one angle.
Rhombus construction given one angle and a diagonal.
Rhombus construction given the altitude and one diagonal.
Part Three:
Show the relationship between the two standard forms of the graph of a parabola:
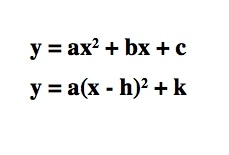
A write-up should show the derivation of one equation from the other AND an interpretation/rationale for the value of parameters a, b, c, h, and k.
Converting From Standard Form to Vertex Form (General Case)

Ex. y =3x² + 4x + 5
Look at the function, we can pull the following information:
a = 3
h = -4/6= -2/3
k = 11/3
Plugging into the Vertex Form we get:
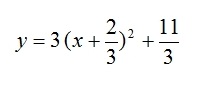
If this is correct, both equations should yield the same graph. Let's graph equation in Graphing calculator.
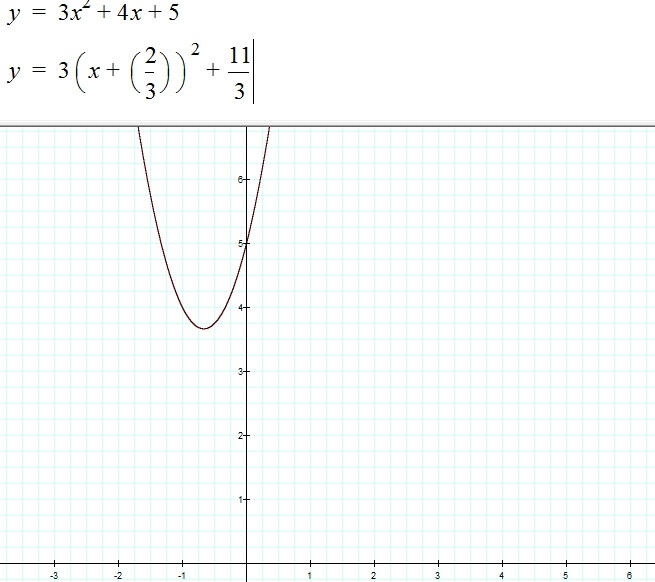
Yes, it is!
Converting From Vertex Form to Standard Form (General Case)

Ex. y = 2(x- 2)² + 5
a = 2
b = -8
c = 13
Plugging into Standard for we get:
y = 2x²-8x+13
If this is correct, both equations should yield the same graph. Let's graph equation in Graphing calculator.
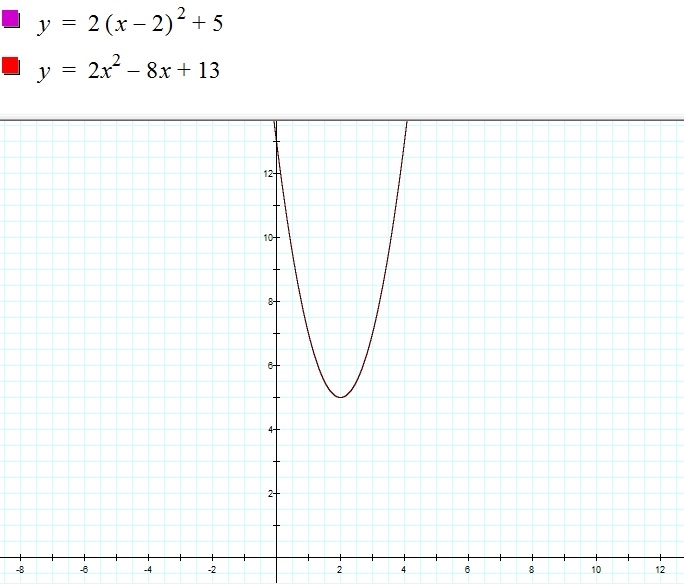
Yes, it is!
To sum, both forms yield the same solution set for quadratic functions. But it has been my experience that students rather graphing parabolas written in vertex form.