

Assignment 4:
Investigating the Perpendicular Bisectors of a Triangle Algebraically
by
Ángel M. Carreras Jusino
Goal: Investigate the properties of the perpendicular bisectors of a triangle algebraically.
Our first goal is to ensure that the perpendicular bisectors intercept at the same point (the circumcenter).
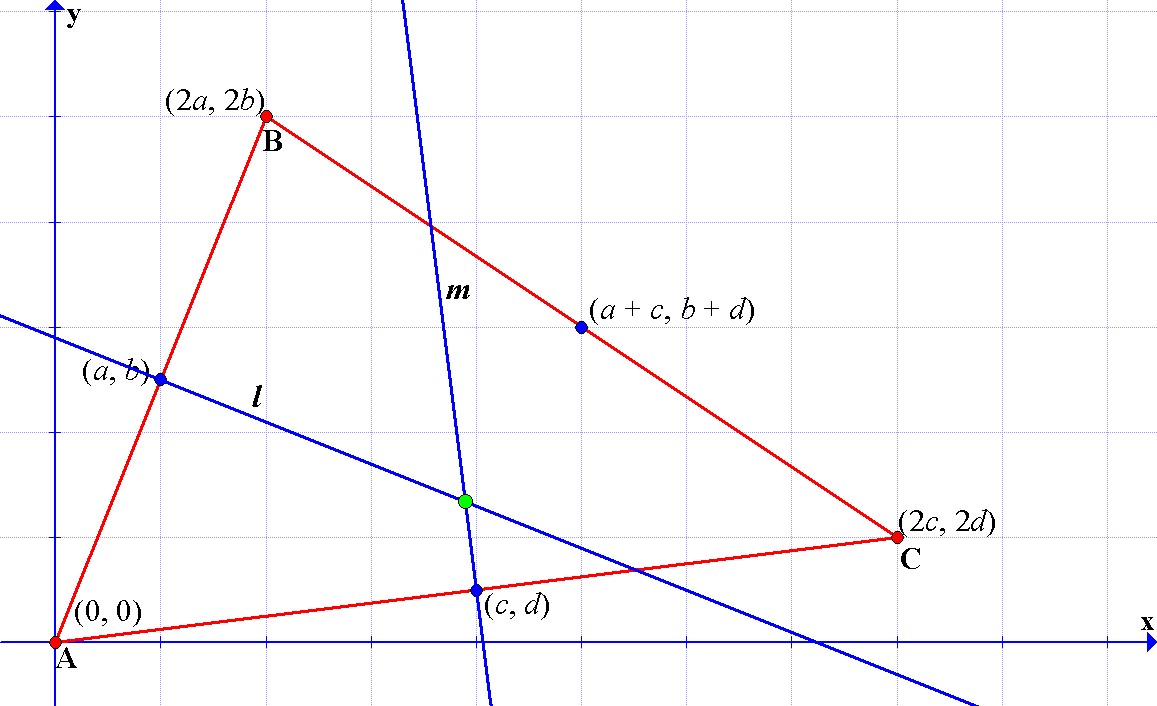
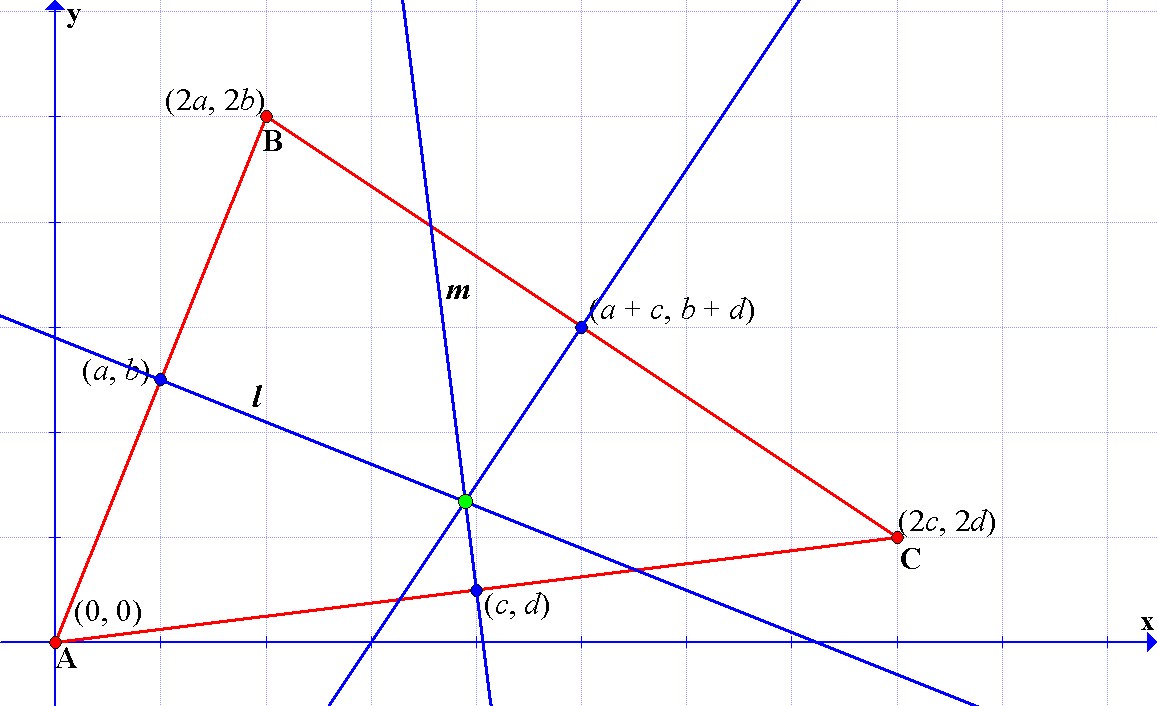
We will begin by constructing a generic triangle in x-y plane with one of its vertices at the origin and the other two vertices at the points (2a, 2b) and (2c, 2d).
Now, we find the midpoint of each side of the triangle.
Next, we find the equations for each perpendicular bisector.
Let begin with the perpendicular bisector of the segment AB, first the slope of the segment AB is
![]()
Hence the slope of its perpendicular bisector is given by
![]() .
.
We know that this line contains the point (a, b), so its equation can be written as
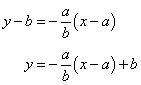
Similarly, can be found that the equation for the perpendicular bisector of the segment AC is given by
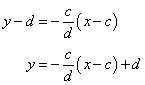
In the case of the perpendicular bisector of the segment BC, the slope of the segment BC is
![]()
Hence the slope of its perpendicular bisector is given by
![]()
Now this perpendicular bisector contains the point (a + c, b + d), so its equation can be written as
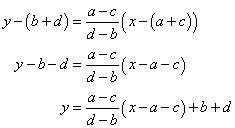
Having the equations of the perpendicular bisectors we can find, algebraically, were they intercept each other.
Let begin by first finding the interception of the perpendicular bisectors of the segments AB and AC, lets call these perpendicular bisectors l and m, respectively.
Now we equate the equations for lines l and m to find the x coordinate of their point of interception.
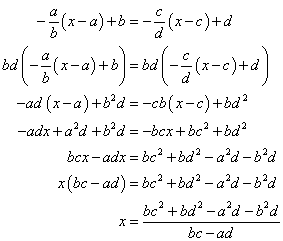
Substituting this value of x in the equation of l or m we can find the y coordinate and thus the coordinates of the point of interception.
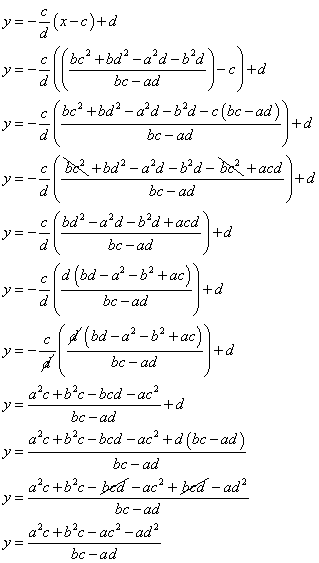
Hence lines l and m meet at the point
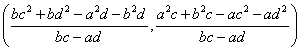
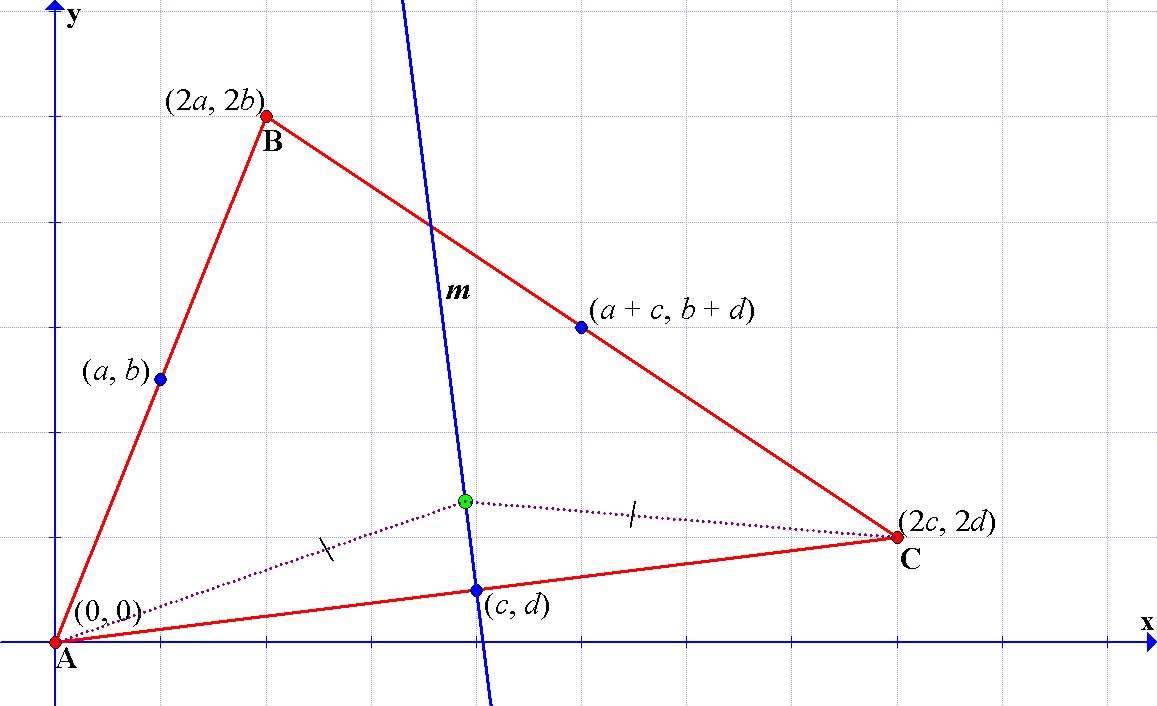
Now that we know the coordinates of the point of interception of lines l and m, we have to check that it also lies on the perpendicular bisector of the segment BC.~
Therefore, the perpendicular bisectors of a triangle are always concurrent.
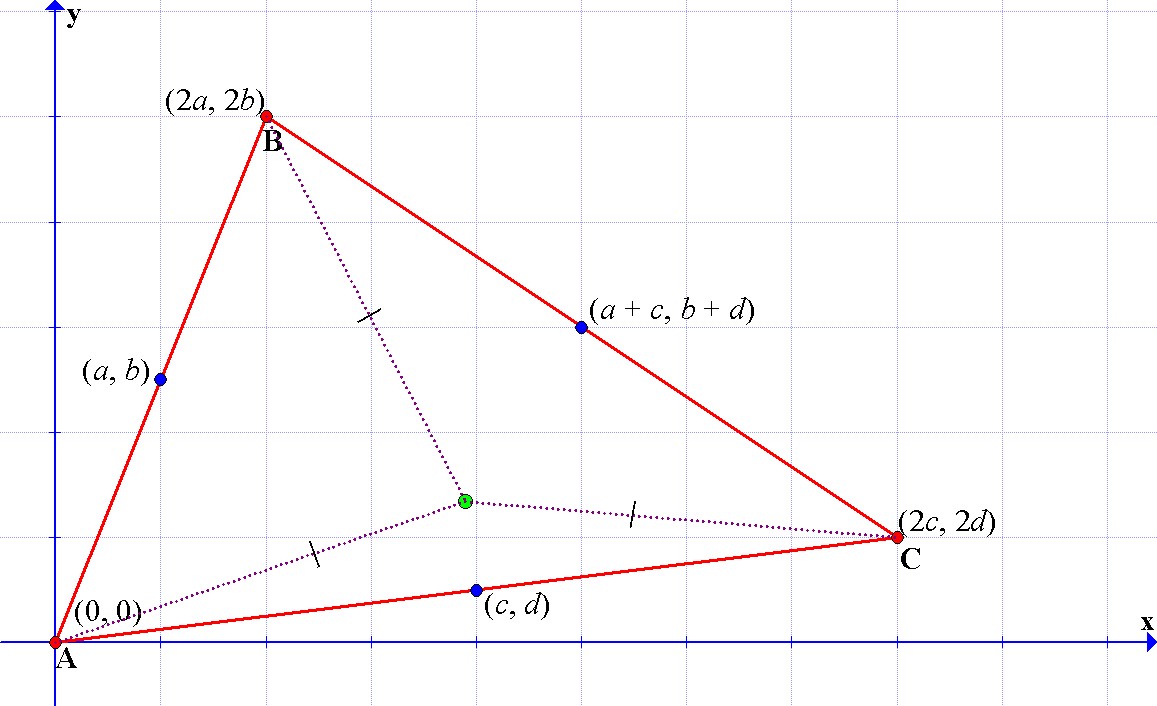
Our second goal is to show that the point of concurrence of the perpendicular bisectors is equidistant from all the vertices of the triangle.
Any point in the perpendicular bisector of a segment is equidistant from the endpoints of the segment.
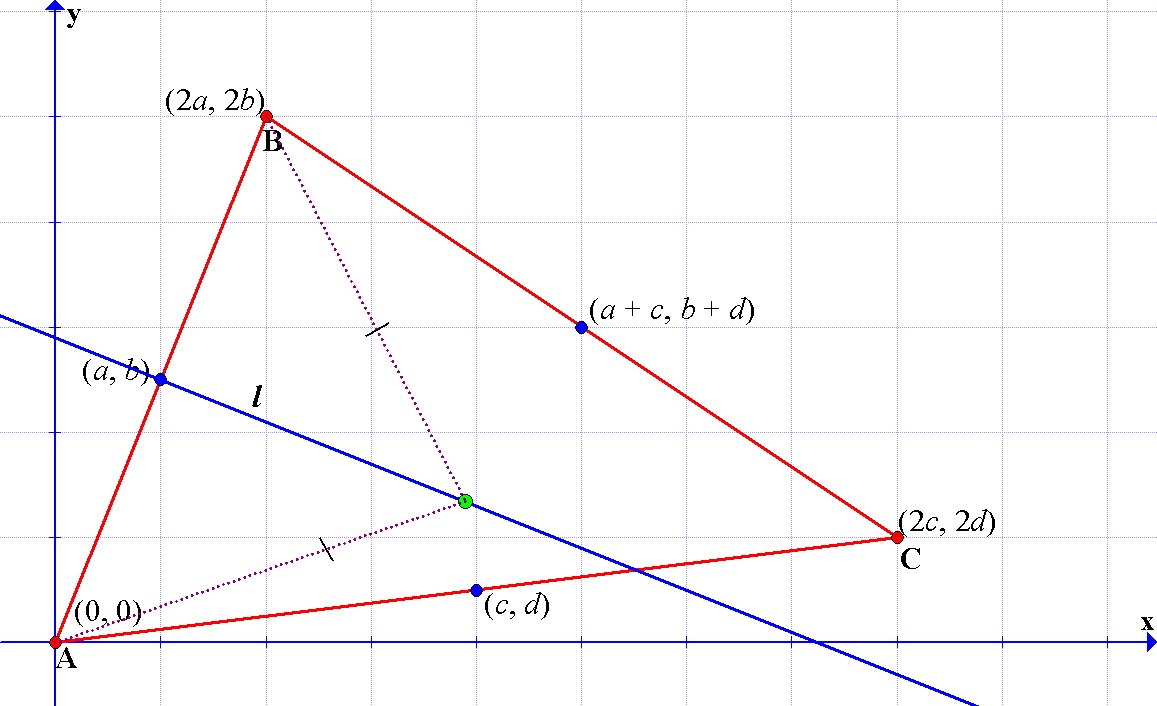

Therefore, the point of concurrence of the perpendicular bisectors is equidistant from the vertices of the triangle.
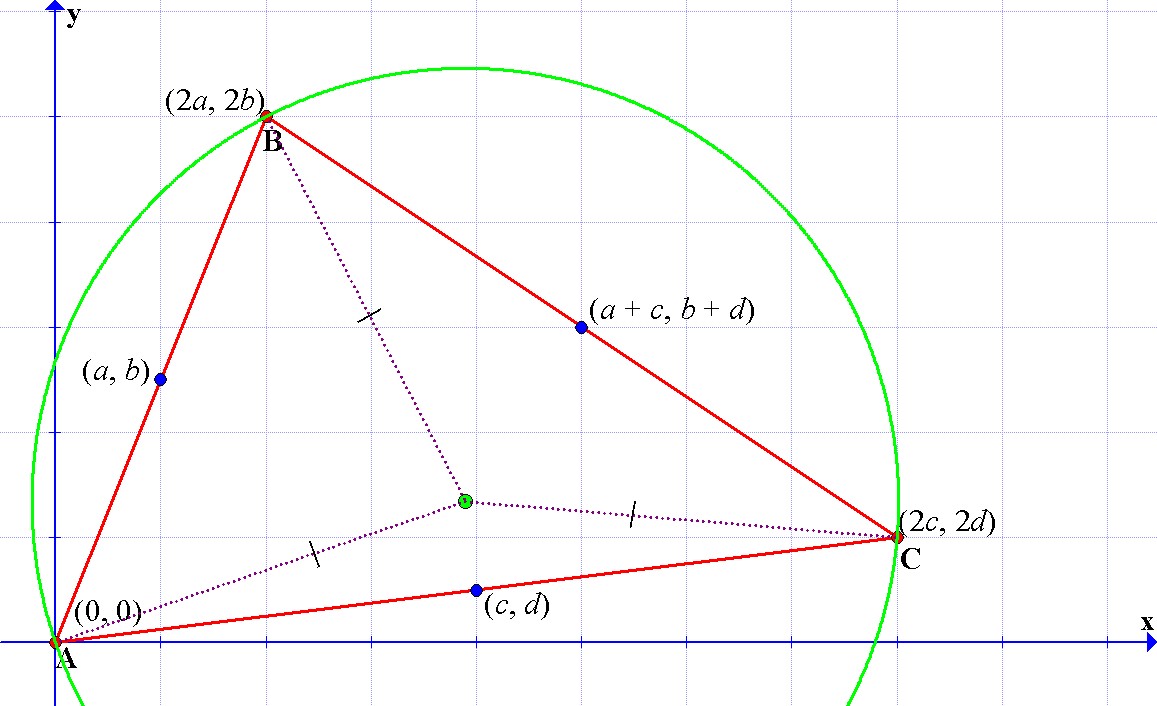
As a result, there exist a circle (the circumcircle) with center at the concurrence point (the circumcenter) that pass through all the vertices of the triangle.
Our last goal is to see if there is any occasion were the circumcenter is not defined based in its already determined coordinate
![]()
The expression for the coordinate is undefined when bc – ad = 0
Case 1. a, b = 0
In this case point B would coincide with point A, therefore there would be no triangle.
Case 2. c, d = 0
Point C would coincide with point A, therefore there would be no triangle.
Case 3. a, c = 0
Point A, B, and C would lie in the y-axis, therefore there would be no triangle.
Case 4. b, d = 0
Point A, B, and C would lie in the x-axis, therefore there would be no triangle.
Case 5.
This implies that the slopes of the segments AB and AC would be the same, hence colinear, therefore there would be no triangle.
Therefore, if ABC is a triangle then its circumcenter is defined.