---

Assignment 6:

Investigating the Relationship between the Area of a Triangle and the Area of the Triangle formed by its Medians

by

Ángel M. Carreras Jusino

Goal: Prove that the area of a triangle formed by the medians of a given triangle is ¾ the area of the given triangle .

Exploration

In the following applet is shown

• triangle ABC with its medians
• triangle GHI (the triangle formed with the medians of triangle ABC)
• the areas of ABC and GHI
• the result of multiplying the area of ABC by ¾.

Drag any of the vertices of triangle ABC and see what happens to the values of the areas and the result of the calculation.

Please install Java (version 1.4 or later) to use JavaSketchpad applets. 

You should note that the area of the triangle of medians is ¾ the area of the original triangle.

Algebraic Proof

Now we are going to prove what was noted during the exploration. Consider the following triangle ABC. In this triangle D, E, and F are the midpoints of the segments BC, AC, and AB respectively. Therefore AD, BE, and CF are the medians of triangle ABC.

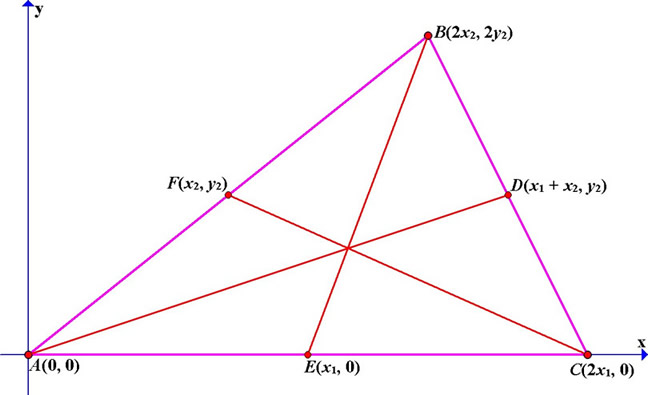
First, we want to find an expression for the area of triangle ABC, note that the triangle has base 2x₁ and height 2y₂. Using the area formula for a triangle we have

A = ½(base)(height) = ½(2x₁)(2y₂) = 2x₁y₂

Now we need to find an expresion for the area of the triangle formed by the medians of triangle ABC, i.e., the triangle with side lengths equal to the lengths of the segments AD, BE, and CF. Since we can't determine the area of the triangle of medians as we did with triangle ABC, we are going to use Heron's formula to find it.

Heron's formula states that the area A of a triangle whose sides have lengths a, b, and c is

where s is the semiperimeter of the triangle

.

This formula can also be written as

.

This version of Heron's formula is what we are going to use for the proof.

Using the distance formula we can find the lengths of the medians, which are going to be the sides of the triangle of medians. So, the area of the triangle of medians is going to be

The lengths of the medians are

Substituing and simplifying for each of the pieces needed for the Heron's formula we get

Therefore the area of the triangle of medians is

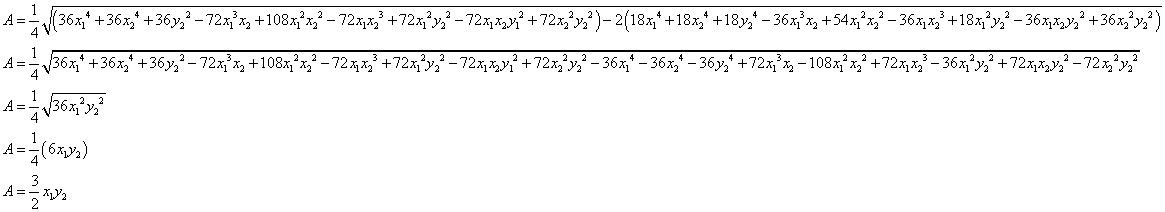
We originally have that triangle ABC has an area of 2x₁y₂ and now we have that the area of the triangle of medians is .

∴ 

Return to Angel's Homepage

Return to EMAT 6880 Page