

Assignment # 1
Explorations with Linear Functions
by
Michael Ferra
Proposed Investigation
Make up linear functions f(x) and g(x). Explore, with different pairs of f(x) and g(x) the graphs for:
i. h(x) = f(x) + g(x)
ii. h(x) = f(x)∙g(x)
iii. h(x) = f(x)/g(x)
iv. h(x) = f(g(x))
Summarize, explain, and illustrate.
i. Adding Linear Functions
Let's begin by observing a couple of pairs of f(x) and g(x) to show h(x) = f(x) + g(x).
1. Let f(x) = 6x + 2 and g(x) = 2x + 3; the rate of change of f(x) is 6 and the rate of change of g(x) is 2. (**Note we can use the following graphical representation of these two linear equations under section ii, iii, and iv as well.)
h(x) = (6x + 2) + (2x + 3)
h(x) = (6x + 2x) + (2 + 3)
h(x) = 8x + 5; summing the two linear functions results in this linear function h(x) with rate of change 8.
2. Let f(x) = 2x - 9 and g(x) = -3x + 7; the rate of change of f(x) is 2 and the rate of change of g(x) is -3. (**Note we can use the following graphical representation of these two linear equations under section ii, iii, and iv as well.)
h(x) = (2x - 9) + (-3x + 7)
h(x) = (2x - 3x) + (-9 + 7)
h(x) = -x - 2; summing the two linear functions results in this linear function h(x) with rate of change -1.
Linear functions can be expressed in the form y = mx + b where m and b are constants. Thus looking at the sum of our sets of two linear functions we can notice that h(x) has the form y = mx + b where the value for m indicates the functions slope or rate of change with respect to x. In our observation of these specific sets, we can observe that when we add two linear functions, the resulting sum has a constant rate of change equal to the sum of the two linear functions.
Let's observe the general case to show that the sum of linear functions is linear.
Let f(x) = m1x + b1 and g(x) = m2x + b2. Solve when h(x) = f(x) + g(x).
h(x) = (m1x + b1) + (m2x + b2)
h(x) = (m1x + m2x) + (b1 + b2)
h(x) = (m1 + m2)x + (b1 + b2)
allow m = m1 + m2 and b = b1 + b2 thus
h(x) = mx + b, the form a linear equation.
Thus the sum of linear functions is a linear equation with a rate of change equal to the sum of the rates of change of the original linear functions.
Click here to create your own linear functions of f(x) and g(x) and see the resulting h(x)!
ii. Multiplying Linear Functions
Let's begin by observing a the same two pairs of linear functions f(x) and g(x) to show h(x) = f(x)g(x).
1. Let f(x) = 6x + 2 and g(x) = 2x + 3; the rate of change of f(x) is 6 and the rate of change of g(x) is 2.
h(x) = (6x + 2) • (2x + 3)
h(x) = (6x + 2) • 2x + (6x + 2) • 3
h(x) = 12x2 + 4x + 18x + 6
h(x) = 12x2 + 22x + 6; let's observe the rate of change
when x = 0, h(x) = 6
when x = 1, h(x) = 40 -- a change of 34 from when x = 0
when x = 2, h(x) = 98 -- a change of 58 from when x = 1
Thus in this function, the rate of change of h(x) with respect to x is not constant, thus not a linear function for this instance.
2. Let f(x) = 2x - 9 and g(x) = -3x + 7; the rate of change of f(x) is 2 and the rate of change of g(x) is -3.
h(x) = (2x - 9) • (-3x + 7)
h(x) = (2x - 9) • -3x + (2x - 9) • 7
h(x) = -6x2 + 27x + 14x - 63
h(x) = -6x2 + 41x - 63; let's observe the rate of change
when x = 0, h(x) = -63
when x = 1, h(x) = -28 a change of 35 from when x = 0
when x = 2, h(x) = -5 a change of 23 from when x = 1
Thus in this function, the rate of change of h(x) with respect to x is not constant, thus not a linear function for this instance.
The product of two linear functions results in a quadratic equation expressed in the form y = Ax2 + Bx + C, where A, B and C are constants. Thus looking at the product of our sets of linear functions we can notice that h(x) has the form y = Ax2 + Bx + C where the rate of change is not defined by a constant value with respect to x. The illustration of the product of two linear equations is a parabola. Notice the parabola crosses the x-axis at two different points, i.e. has two x-intercepts called roots. Our linear functions have only one x-intercept and is defined when y = 0. Since the quadratic equation is the product of two linear functions, then we can see the quadratic equation having the x-intercepts defined by our two linear equations.
Let's for the fun of it, observe the general case of the product of two linear functions to show it results in the form of a quadratic equation.
Let f(x) = m1x + b1 and g(x) = m2x + b2. Solve when h(x) = f(x) • g(x).
h(x) = (m1x + b1) • (m2x + b2)
h(x) = (m1x + b1) • m2x + (m1x + b1) • b2
h(x) = m1m2x2 + m2b1x + m1b2x + b1b2
h(x) = m1m2x2 + (m2b1 + m1b2)x + b1b2
allow A = m1m2, B = m2b1 + m1b2, and C = b1b2 thus
h(x) = Ax2 + Bx + C, the form of a quadratic equation.
Thus the product of two linear functions is a quadratic equation.
Click here to create your own linear functions of f(x) and g(x) and see the resulting h(x)!
iii. Dividing Two Linear Functions
Let's begin by observing our same two pairs of linear functions f(x) and g(x) to show h(x) = f(x)/g(x).
1. Let f(x) = 6x + 2 and g(x) = 2x + 3.
h(x) = (6x + 2)/(2x + 3)
As we did with multiplying the two linear functions, we can determine that the rate of change of dividing two linear functions is not constant with respect to x, thus not linear.
For this specific case, the result of dividing the two linear equations gives us a function of the ratios of the two linear equations. Thus this is a rational function and more specifically a hyperbola.
Observing the graph of the hyperbola we can notice that the hyperbola approaches, but never reaches, two lines. These lines are called asymptotes and be found using our two linear functions. The denominator of h(x) can tell us where h(x) doesn't exist, giving us our vertical asymptote. This is simply done by setting the denominator equal to zero since we know dividing by zero is undefined.
2x + 3 = 0
2x = -3
x = -3/2
To find the other asymptote, which will be horizontal, we solve for the inverse of h(x) and set it's denominator equal to zero as well. Allow h(x) to be represented as y to solve for the inverse.
y = (6x + 2)/(2x + 3)
y(2x + 3) = (6x + 2)
2xy + 3y = 6x + 2
2xy - 6x = 2 - 3y
x(2y - 6) = (2 - 3y)
x = (2 - 3y)/(2y - 6)
Now that we've found the inverse, let's set it's denominator equal to zero to find our undefined value for x.
2y - 6 = 0
2y = 6
y = 3
2. Let f(x) = 2x - 9 and g(x) = -3x + 7; the rate of change of f(x) is 2 and the rate of change of g(x) is -3.
h(x) = (2x - 9)/ (-3x + 7)
Once again, for this specific case, the result of dividing the two linear equations gives us a function of the ratios of the two linear equations. Thus this is a rational function and more specifically a hyperbola.
Solving for the two asymptotes can be done in the same manner. For this function, we will find our boundary lines to be defined by the two equations x = 7/3 and y = -2/3.
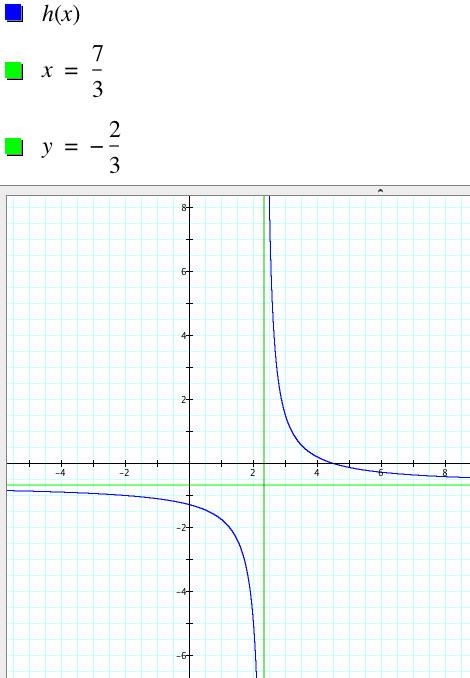
The quotient of two linear functions results in a rational equation which can be expressed as the ratio of two polynomial functions. Since we are dealing with one variable, we can write this in the form k(x) = p(x)/q(x), where q(x) ≠ 0. Even more specifically, since we are dealing with linear equations, we can express this as y = (m1x + b1)/(m2x + b2). Thus looking at the quotient of our sets of linear functions we can notice that h(x) has the form y = (m1x + b1)/(m2x + b2).
Once again, for the fun of it, let's observe the general case of the quotient of two linear functions to show the asymptotes of the equation.
Let f(x) = m1x + b1 and g(x) = m2x + b2. Solve when h(x) = f(x)/g(x).
h(x) = (m1x + b1)/(m2x + b2)
Let's set the denominator equal to zero since we know the equation is undefined at this value.
(m2x + b2) = 0
m2x = -b2
x = (-b2)/(m2); this is our vertical asymptote. Notice it is found by dividing the negative y-intercept of our linear function in the denominator by the slope of the linear equation in the denominator.
To solve for the horizontal asymptote allow h(x) to be represented as y to solve for the inverse.
y = (m1x + b1)/(m2x + b2)
y(m2x + b2) = (m1x + b1)
ym2x + yb2 = m1x + b1
ym2x - m1x = b1 - yb2
x(ym2 - m1) = (b1 - yb2)
x = (b1 - yb2)/(ym2 - m1)
Now that we've found the inverse, let's set it's denominator equal to zero to find our undefined value for x.
ym2 - m1 = 0
ym2 = m1
y = m1/m2; this is our horizontal asymptote. Notice, that using our original h(x), the horizontal asymptote is found by dividing the slope of the linear function in the numerator by the slope of the linear function in the denominator.
Click here to create your own linear functions of f(x) and g(x) and see the resulting h(x)!
iv. Composition of two linear functions
Let's begin by observing our same two pairs of linear functions f(x) and g(x) to show h(x) = f(g(x)).
1. Let f(x) = 6x + 2 and g(x) = 2x + 3; the rate of change of f(x) is 6 and the rate of change of g(x) is 2.
h(x) = 6(2x + 3) + 2
h(x) = 12x + 18 + 2
h(x) = 12x + 20; the composition of the two linear functions results in this linear equation h(x) with rate of change 12.
2. Let f(x) = 2x - 9 and g(x) = -3x + 7; the rate of change of f(x) is 2 and the rate of change of g(x) is -3.
h(x) = 2(-3x + 7) - 9
h(x) = -6x + 14 - 9
h(x) = -6x + 5; the composition of the two linear functions results in this linear equation h(x) with rate of change -6.
Looking at h(x) = f(g(x)), the composition of our sets of two linear functions, we can notice that h(x) has the form y = mx + b where the value for m indicates the functions slope or rate of change with respect to x. In our observation of these specific sets, we can observe that when we compose two linear functions, the resulting value for m is a constant rate of change equal to the product of the slopes from the two linear functions.
Let's observe the general case to show that the composition of linear functions is linear.
Let f(x) = m1x + b1 and g(x) = m2x + b2. Solve when h(x) = f(g(x)).
h(x) = m1(m2x + b2) + b1
h(x) = m1m2x + m1b2 + b1
Since m1, m2, b1, and b2 are constants, allow m = m1m2 and b = m1b2 + b1 thus
h(x) = mx + b, the form a linear equation.
Thus the composition of linear functions is a linear equation with a rate of change equal to the product of the rates of change of the original linear functions.
Click here to create your own linear functions of f(x) and g(x) and see the resulting h(x)!