
Assignment # 9
Explorations with Pedal Triangles
by Michael Ferra
Proposed Investigation
i. Let △ABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of △ABC (extended if necessary) locate three points A', B', C' that are the intersections. △A'B'C' is the Pedal Triangle for Pedal Point P.
ii. What if the pedal point P is the incenter of △ABC?
iii. What if the pedal point P is the circumcenter of △ABC?
iv. What if the pedal point P is the orthocenter of △ABC?
v. Bringing it all together.
i. Let △ABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of △ABC (extended if necessary) locate three points A', B', C' that are the intersections. △A'B'C' is the Pedal Triangle for Pedal Point P.
Let's start by looking at a few examples.
Let's choose a random Pedal point P outside of our original △ABC.
Notice our original △ABC is displayed by the lines and shadings in blue. Choosing a random Pedal Point P outside of our original △ABC we can construct perpendiculars through the point P to the sides of △ABC(extended if necessary). These perpendicular lines are represented by the dashed orange segments. The intersection of the line perpendicular to side BC is labeled A', to side AC is labeled B', and to side AB is labeled C'. These points A', B', and C' are the vertices of our pedal triangle, thus we have △A'B'C'. As seen from the image above, pedal △A'B'C' is depicted by the lines and shadings in green. Notice when the pedal point P is outside the the original △ABC, the Pedal △A'B'C' is shown to be outside of △ABC as well. We will use this same logic to construct future Pedal Triangles given a Pedal Point.
Let's choose a random Pedal Point P inside of our original △ABC.
Notice when the Pedal Point P is inside the original △ABC, the Pedal △A'B'C' is shown to also be inside △ABC.
Click here to change the vertices and to drag the pedal point P wherever you'd like!
ii. What if the pedal point P is the incenter of △ABC?
If we want to observe the pedal point P as the incenter of △ABC, then let's construct △ABC and find the incenter of △ABC.
To find the incenter of △ABC, the angle bisectors of each vertex has been constructed and the point of concurrency is the incenter. Let's label this point P since we want the pedal point to be the incenter of △ABC. Observe the angle bisector also bisects the line opposite to its angle, thus finding the angle bisector of the angle at vertex A, the line constructed also bisects side BC of △ABC. The same can be said of the angle bisectors of vertex B to AC and vertex C to AB.
Now let's construct the perpendiculars to the sides of △ABC through our pedal point P and label the points of intersection.
The lines of the angle bisectors are concurrent at the incenter, point P, thus when creating perpendiculars through point P to the sides of △ABC, we get the figure above. We will label these intersections in the same manner as we did previously.
Now let's show our pedal triangle.
Since we know P is the incenter of △ABC, let's construct the incircle of △ABC just for the fun of it.
Notice the vertices of the pedal triangle, △A'B'C', all lie on the incenter of △ABC. We can thus conclude that the incircle of △ABC is the circumcircle of △A'B'C'. This means that pedal point P is also the circumcenter of △A'B'C'.
Click here to change the vertices A, B, and C and show for any triangle you'd like!
iii. What if the pedal point P is the circumcenter of △ABC?
If we want to observe the pedal point P as the circumcenter of △ABC, then let's construct △ABC and find the circumcenter of △ABC.
To find the circumcenter of △ABC, we must begin by bisecting the sides of △ABC. This gives us the midpoint of each side. Now construct the perpendiculars to each midpoint to its respected side. For example, we have the midpoint of side AB so we will construct a perpendicular line through the midpoint to side AB, i.e. its perpendicular bisector. These three perpendicular bisectors of △ABC are concurrent at the circumcenter of △ABC. Let's label this point P since we want the pedal point to be the circumcenter of △ABC.
Now let's construct the perpendiculars to the sides of △ABC through our pedal point P and label the points of intersection.
Wow!! The perpendicular bisectors of △ABC from our first step look exactly the same as the perpendiculars constructed in our second step. This is because they are the same!
Now let's show our pedal triangle.
We know the midpoints of △ABC are the vertices of the pedal triangle, △A'B'C', thus we can conclude that △A'B'C' is the medial triangle of △ABC.
Let's focus on △A'B'C' for a moment now and observe the altitudes of this triangle.
Notice the altitudes of △A'B'C' are concurrent at the pedal point P. We can thus conclude that P is the orthocenter of △A'B'C'. Thus when the pedal point P is the circumcenter of △ABC, P is also the orthocenter of the pedal triangle.
Click here to change the vertices A, B, and C and show for any triangle you'd like!
iv. What if the pedal point P is the orthocenter of △ABC?
If we want to observe the pedal point P as the orthocenter of △ABC, then let's construct △ABC and find the orthocenter of △ABC.
To find the orthocenter of △ABC, we must find the altitudes of △ABC and find where they are concurrent. To find the altitudes, we construct perpendicular lines through a vertex to it's opposite side. For example, construct a perpendicular line through vertex A to its opposite side BC. Notices these lines intersect. This is the foot of the perpendicular. Thus the altitude is defined as the distance from the vertex A to the foot of the perpendicular. The same construction can be done for the vertices B and C. A more accurate depiction of the altitudes is shown below.
These three altitude of △ABC are concurrent at the orthocenter of △ABC. Let's label this point P since we want the pedal point to be the orthocenter of △ABC.
Now let's construct the perpendiculars to the sides of △ABC through our pedal point P and label the points of intersection. Let's label the points of intersection as well here.
Wow!! The altitudes of △ABC from our first step look exactly the same as the perpendiculars constructed in our second step. This is because they are the same!
Now let's show our pedal triangle.
Since the pedal triangle was constructed using the altitudes of △ABC, the resulting △A'B'C' is the orthic triangle. Not that it is the orthic triangle as long as △ABC is acute.
Let's observe one last interesting detail of this pedal triangle. Let's construct the angle bisectors of △A'B'C' and find its incenter.
Notice when the pedal point P is the orthocenter of △ABC it is also the incenter of the pedal triangle. Too cool!!
Click here to change the vertices A, B, and C and show for any triangle you'd like!
v. Bringing it all together.
Let's begin with the pedal point P as the incenter of △ABC. Once again, let's construct the pedal triangle, △A'B'C'.
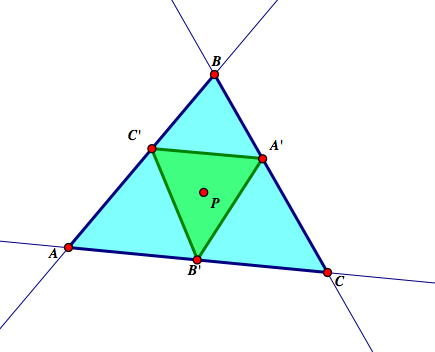
From our previous explorations we know that since the pedal point P of △ABC is the incenter then P is also the circumcenter of △A'B'C'. Now with P being the circumcenter of △A'B'C', let's create the pedal triangle to △A'B'C'.
From our previous explorations we know that since the pedal point P of △A'B'C' is the circumcenter then P is also the orthocenter of △A''B''C''. Now with P being the orthocenter of △A''B''C'', let's create the pedal triangle to △A''B''C''.
From our previous explorations we know that since the pedal point P of △A''B''C'' is the orthocenter then P is also the incenter of △A'''B'''C'''. We are now back to P being the incenter of a triangle. We can thus conclude that △ABC≈△A'''B'''C'''.
Interesting stuff!!