Problem asks us to construct a triangle inscribed in another triangle that has minimum perimeter.

Below is the Construction followed by the proof.

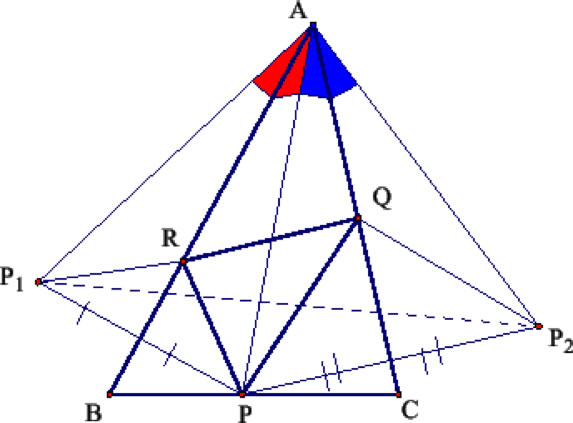
Proof: We will Consider the triangle PQR that is inscribed in the triangle ABC. We obtained P1 by reflecting P across AB and P2 by reflecting P across CA. Since both Triangles PP1R and PQP2 are isoceles,

We can conclude that RP1=RP and that PQ=P2Q.

Hence P1RQP2 is equivalent to the the perimeter of  Triangle PQR.

By fixing P and varying the position of  R and Q along AB and CA until they like on P1P2, the perimeter of PQR is equal to P1P2.

Because P1AP and P2AP are isoceles, AP1=AP=AP2.

Also, Angle P1AP2 is twice the measure of angle A, because AB is the Bisector of angle P1AP and AC is the the bisector of angle PAP2.

By allowing letting R and Q on P1P2 and moving P along BC, angle P1AP remains constant with a measure twice the measure of A.

Furthermore, Triangle P1AP2 remains isoceles.

P1P2 however varies in direct proportion to AP. Thus P1P2 will be at its minimum when AP is at its minimum  which happens when AP is the altitude of ABC to the side BC.

Therefore the triangle has minimum perimeter because two of its sides are at their minimum.

This triangle is Called ORTHIC TRIANGLE.

 

SOMTHING TO THINK ABOUT :

Below is this sculpture that stands outside the Department of Mathematics at Hope college. Would you consider the inscribed triangle an Orthic triangle ?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

source:wichita state university mathematics.