

Mary Ellen Graves
Assignment 6: Minimum Perimeter of an Inscribed Triangle
Below is ΔABC with dropped altitudes from each vertice. After, a few runs of 'trial and error it was concluded that the foot of the dropped altitudes gives the vertices of the inscribed triangle with minimum perimeter.
ΔDEF is the triangle created by the foot of the altitudes dropped from the vertices of the original triangle ΔABC. This triangle has minimum perimeter, but what happens when ΔABC is no longer an acute triangle? What happens when it is a right triangle? And what happens when it is an obtuse triangle?
First, let's refresh our memories on the proof of the minimum perimeter of an inscribed triangle which we will see is the orthic triangle formed by the feet of the altitudes dropped from the vertices.
PROOF: Here we have ΔABC with an arbitrary ΔDEF inscribed within ΔAB. Draw a segment from vertex C to our point D on segment AB. Now if we reflect CD across the segment AC and reflect CD across BC we find that we have two additional triangles ΔCDD' and ΔCD''D. Because CD' is a reflection of CD we know they are congruent. Similarly, because CD' is the reflection of CD they too are congruent. Therefore, ΔCDD' and ΔCD''D are isosceles triangles. We can then see that the ∠D'CD'' = 2∠C= 2∠DCA + 2∠DCB. Hence, CA is the angle bisector of ∠D'CD and CB is the angle bisector of ∠DCD''. Now that we have two isosceles triangles with known angles we can proceed to find the minimum perimeter of the inscribed triangle. With the isosceles triangles and angle bisectors we can see that DF = FD'' and DE = D'E. For the perimeter to be the minimum we must find where the segments D'E, EF, and FD'' lie along a straight line. Once they lie along a straight line we will see that the segment length D'D'' is our minimum perimeter because ΔD'CD'' is an isosceles and directly proportionate to the segment CD. Therefore, when CD is at a minimum then D'D'' will be at a minimum.
Finally, we can see that CD is at a minimum when CD is the altitude of vertex C. A similar proof follows for showing that E and F are also the feet of the altitudes dropped from the remaining vertices. In conclusion, the orthic triangle formed by the feet of the altitudes of a triangle ΔABC is also the triangle inscribed with minimum perimeter.
Our explorations continue to search what happens to the orthic triangle with minimum perimeter inscribed in ΔABC when ΔABC is an obtuse triangle or a right triangle. First, take a look at the picture below. This is the inscribed orthic triangle ΔDEF directly before the ∠C becomes an obtuse angle. Can you take a guess as to what happens when the ∠C is no longer acute?
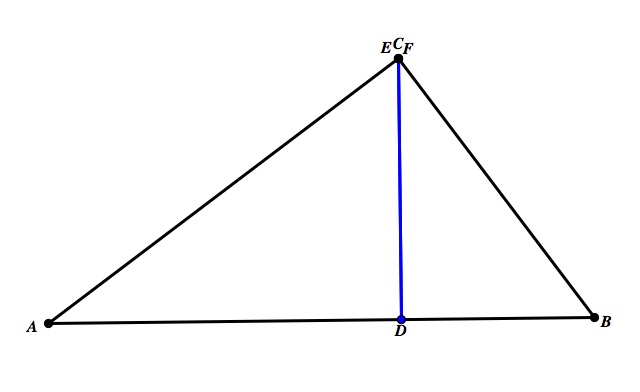
Yes, you guessed it. The orthic triangle disappears completely. The orthocenter, which is the center of the inscribed circle in ΔABC, lies outside of an obtuse triangle and the segments of ΔDEF no longer form the orthic triangle. However, their extended lines are concurrent, but since there is no longer an orthic triangle formed by the altitudes of ΔABC there no longer exists an inscribed triangle with minimum perimeter. The word 'inscribed' is a good indication that there does not exist an orthic triangle for an obtuse triangle when the orthocenter lies outside the triangle.
Continuing with our explorations of orthic triangles with different triangles, lets look what happens to ΔDEF when ΔABC is a right triangle.
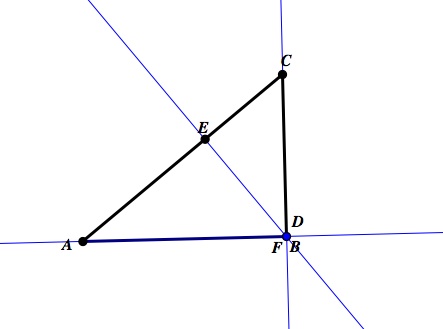
It was not necessary for a graph of the altitudes of a right triangle. Using our intuition and comprehension of altitudes and right triangles we would know that two of our altitudes dropped from two vertices will be concurrent with two sides of ΔABC. We can see in our picture, like in an obtuse triangle, that the orthic triangle ceases to exist in a right triangle. In a right triangle, the orthocenter lies on the triangle making it impossible to form an inscribed triangle with minimum perimeter. In conclusion, the triangle inscribed inside ΔABC with minimum perimeter is in fact the orthic triangle which is formed by dropping the altitudes from each vertex of ΔABC where the feet of the altitudes become the vertices of the inscribed triangle with minimum perimeter. A triangle with minimum perimeter inscribed in ΔABC will only exists when ΔABC is an acute triangle.
CLICK HERE TO RETURN TO MY HOME PAGE