

Recall that a point on a conic graph is a distance r from the focus and a distance kr from a directrix. If k< 0 an ellipse is obtained. For k = 1, the parabola is obtained. For k > 1 the result is the hyperbola. Let the focus be at the origin and and the directrix be a vertical line at - p, where p>0.
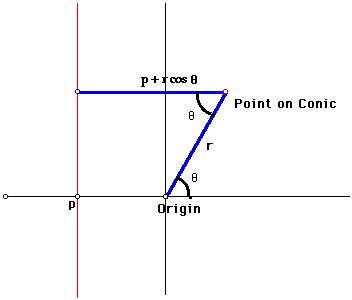
The distance from a point on the conic to the vertical line p can be expressed as
Now from the definition of conics
[Note: Use this equation to explore graphs using Graphing Calculator 3.5. This program does not require solving for r first.]
Now, solve for r. The polar form of a conic results.
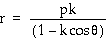
The other forms of the equation can be found by considering cases where the vertical line is at +p or where horizontal lines at +p or - p are considered.