

Last modified on July 26, 2014.
Write-Up #6
Examine each of the following 11 explorations. Select any one or a combination of them for a write-up.
1. Construct a triangle and its medians. Construct a second triangle with the three sides having the lengths of the three medians from your first triangle. Find some relationship between the two triangles. (E.g., are they congruent? similar? have same area? same perimeter? ratio of areas? ratio or perimeters?) Prove whatever you find. See Java GSP construction
Prove the area of the triangle of medians is
the area of the original triangle.
If the original triangle is equilateral, then the triangle of medians is equilateral. Will an isosceles original triangle generate and isosceles triangle of medians? Will a right triangle always generate a right triangle of medians? What if the medians triangle is a right triangle? Under what conditions will the original triangle and the medians triangle both be right triangles?
2.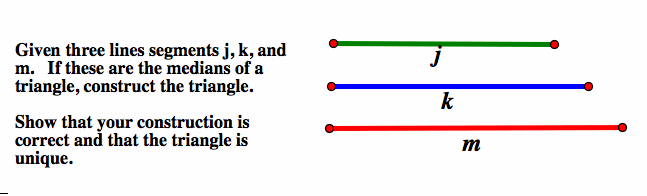
3. A 4 by 4 picture hangs on a wall such that its bottom edge is 2 ft above your eye level. How far back from the picture should you stand, directly in front of the picture, in order to view the picture under the maximum angle? Side view:
4. The football rules in college football were changed a few years ago to make the uprights about 5 feet narrower than previously. Many game commentators have harped about how much harder it is to kick field goals from the hash marks. Assume the field goal is attempted from the hash marks. At what yard marker does the kicker have maximum angle to the two uprights? In college football today, the width of the goal posts is 18 ft. 6 in. and the width of the hash marks is 40 ft. Make a sketchpad model similar to the one below. Is there any merit to some commentators argument to take a penalty in order to have a "better angle" on the field goal kick when the ball is close to the goal line?
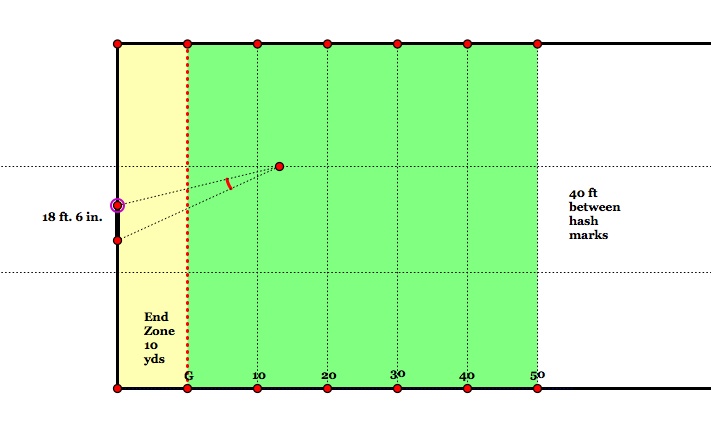
In High School football, the width of the goal posts is 23 ft. 4 in. and the distance between the hash marks is 53 ft. 4 in. Is the kicking angle "better" in high school football than in college football? Is there a point along the hash mark in high school football where a better kick angle is obtained by taking a 5 yd penalty?
5. Given three points A, B, and C. Construct a line intersecting AC in the point X and BC in the point Y such that
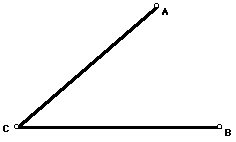
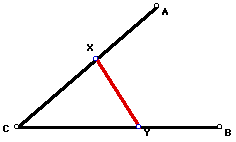
Prove your construction is valid. (Measurement is not a means of mathematical proof. "Draging" with GSP is not a means of mathematical proof.)
6. Construct the common tangents to two given circles. Make a script tool. Test it for all the different cases. Or, do you need different script tools for the different cases?
Discuss your constructions and prove they are valid.
7. Of a triangle, given two vertices A and B, and the angle at the third vertex C (the angle opposite side AB). What is the locus of the point C? See Script # 19 in Assignment 5.
(Note: Think of this as turning a fixed angle so that its sides always rest on the two endpoints of the segment AB. Remember that the size of the angle is fixed but the sides can move along A and B simultaneously.)
8. A parabola is the set of points equidistant from a line, called the directrix, and a fixed point,called the focus. Assume the focus is not on the line. Construct a parabola given a fixed point for the focus and a line (segment) for the directrix.
a. Use an Action Button to generate the parabola from an animation and trace of a constructed point.
b. Repeat 9a with a trace of the tangent line at the constructed point.
c. Use the locus command to generate the parabola from a constructed point or the tangent line at that point.
9. Construct the locus of points equidistant from a fixed point F and a circle. In other words, repeat the parabola construction but use a circle as the "directrix." Let F be any point in the plane other than the center of the circle. Assume F is not on the circle; it can be either inside or outside.
10. Consider any triangle ABC. Find a construction for a point P such that the sum of the distances from P to each of the three vertices is a minimum.
11.Construct the triangle with minimum perimeter inscribed in a given triangle.