

Perform the following constructions
a. Construct any triangle ABC.
b. Construct the Orthocenter H of triangle ABC.
c. Construct the Orthocenter of triangle HBC.
d. Construct the Orthocenter of triangle HAB.
e. Construct the Orthocenter of triangle HAC.
f. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.
1. Conjectures? Proofs?
Does your contruction look something like this? Click HERE for another drawing with the line of the altitudes showing.
What would happen if any vertex of the triangle ABC was move to where the orthocenter H is located? Where would H then be located? Click HERE for a GSP file with "move" buttons to see these animations? Explanation? Interpretation?
2. Construct the nine point circles for triangles ABC, HBC, HAC, and HAB. Conjecture? Proof?
3. Construct triangle ABC, its incircle, its three excircles, and its nine-point circle. Conjecture? Proof?
The triangle has the incircle in black and the three excircles in blue. The nine-poi9nt circle is the maroon circle. Feurebach's conjecture (theorem) holds that the nine-point circle is tangent to each of the three excircles and the incircle.Click HERE for a GSP file.
4. Examine the triangle formed by the points where the extended altitudes meet the circumcircle. How is it related to the Orthic triangle? Proof?
a. Construct your own GSP sketch.
b. Click HERE for a picture to compare with your construction.
c. Click HERE for GSP sketch to manipulate.
Will the relationship still hold if the original triangle is obtuse? Note that in order to construct the altitudes of an obtuse triangle the sides adjacent to the obtuse angle must be extended.
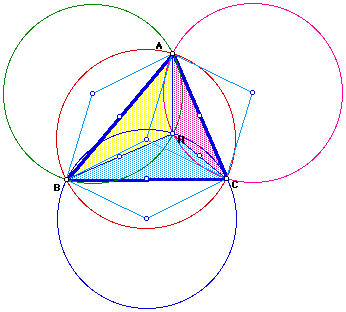
5. Construct any acute triangle ABC and its circumcircle. Construct the three altitudes AD, BE, and CF. Extend each altitude to its intersection with the circumcircle at corresponding points P, Q, and R.
Find
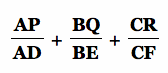
and prove your result. Click HERE for a GSP sketch to manipulate.
6.
Given acute triangle ABC. Construct the Orthocenter H. Let points D, E, and F be the feet of the perpendiculars from A, B, and C respectfully.
Click HERE for a GSP sketch. What if ABC is an obtuse triangle?
7. The internal angle bisectors of triangle ABC are extended to meet the circumcircle at points L, M, and N, respectively. Find the angles of triangle LMN in terms of the angles A, B, and C. Does your result hold only for acute triangles?
8. Construct triangle ABC, its orthocenter H, and the circumcircle for triangle ABH. Use AB as "mirror" to reflect triangle ABC. Does this suggest a proof of any of the previous conjectures?
9. Find the triangle of minimal perimeter that can be inscribed in a given triangle. (For a start, you may want to restrict your investigation to the given triangle being acute.)
At the right, triangle DEF is inscribed in triangle ABC. Reflecting point D in AB to locate image D' and in AC to locate image D" we have a broken line D'FED" that has the same total length as the perimeter of triangle DEF. Can we find conditions on locating D, E, and F so that the points D', F, E, and D" are collinear?