NTRODUCTION:

In this discussion we wish to start by taking a look at the expression as the integer value of k is varied and a and b are equal. First consider the following graphs:

RED-

BLUE-

GREEN-

YELLOW-

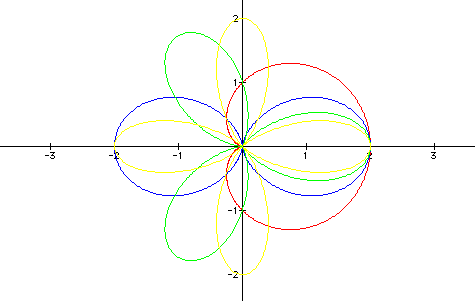
As you can see, the integer value of k determines the number of "petals" on the figure in the graph. You can probably imagine that as k continues to increase the number of petals will also increase.

If we were to change the expression to and still vary the value of k then the graph would look like this:

RED-

BLUE-

GREEN-

YELLOW-

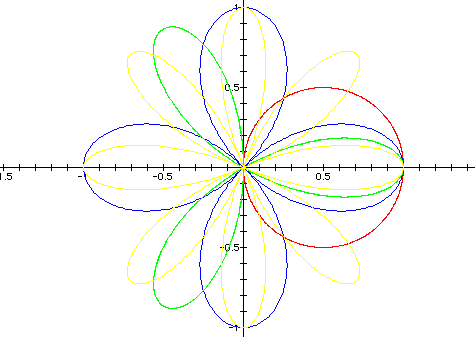
In this case, if k is odd then there are k "petals" in the figure and if k is even then there are 2k "petals" in the figure.

Now we will take the original equation, , and replace cos with sin and see how this effects the graph. So here is the graph of for the given integer values of k.

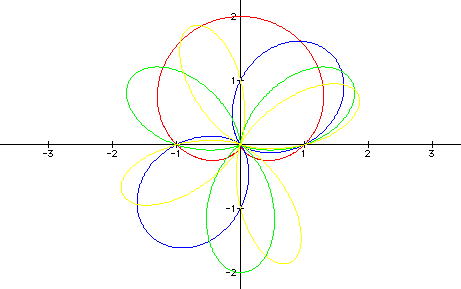
So, now we can see that by switching from sin to cos the graph is rotated. To get a little better picture here is a graph of the equation using sine over the graph using cosine:

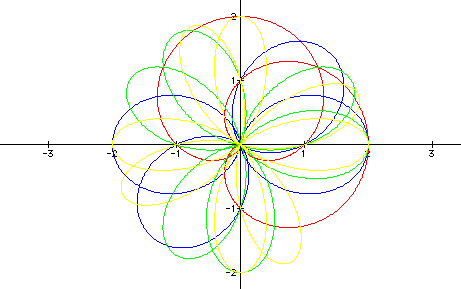
It may be a little difficult to decipher between the two graphs but you should be able to tell that the rotation is not the same for every value of k. For example, when k=1 the graph using sine is a 90 degree rotation of the graph using cosine. And when k=2 the graph using sine is a 45 degree rotation of the graph using cosine. To be more precise, when using sine the graph is a rotation by 90/k degrees from the graph using cosine.