In the following investigation
I will take a look at the various centers of a triangle while
gaining a better understanding of the workings of GSP.
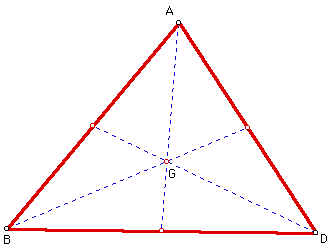
First let's consider the centroid of a triangle. The CENTROID (G) of a triangle ABD is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the oppostie side.

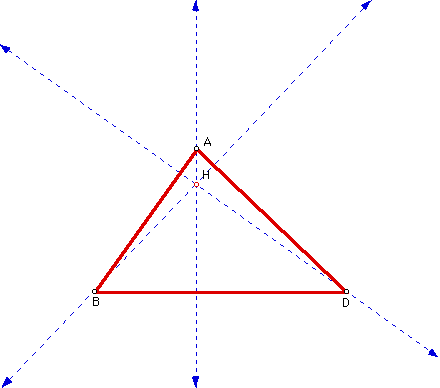
Now let's take a look at the orthocenter of a triangle. The ORTHOCENTER (H) of a triangle ABD is the common intersectiong of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side.
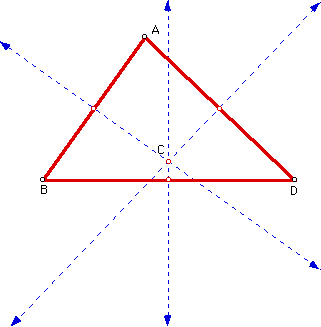
Next let's look at the circumcenter. The CIRCUMCENTER (C) of a triangle ABD is the point in the plane equidistant from the three vertices of the triangle. Since a point equidistant from two points lies on the perpendicular bisector of the segment determined by two points, C is on the perpendicular bisector of each side fo the triangle.
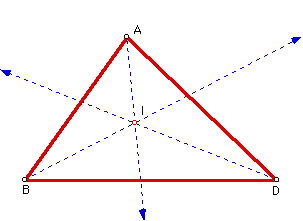
Last, let's consider the incenter. The INCENTER (I) of a triangle is the point on the interior of the triangle that is equidistant from the three sides. Since the point interior to an angle that is equidistant from th two sides of the angle lies ont eh angle bisector, then I must be on the angle bisector of each angle of the triangle.
Now that we have taken a look at each of the three centers it would be nice to prove something about them. In each case we are assuming that the necessary lines are concurrent when we show the given center. However, it is useful to prove that the lines are concurrent. At this point we will prove that the perpendicular bisectors of a triangle are concurrent and thus the circumcenter does exist.

PROOF:
We know that if two lines are not parallel then they will intersect in one exactly one point. If the two lines are parallel then they could intersect in infinitely many points or not at all. In triangle ABD the only way that any of the perpendicular bisectors could be parallel is if two sides of the triangle are parallel. This is impossible because it refutes the definition of a triangle. Therefore we know that each pair of perpendicular bisectors intersect in exactly one point. It is left to show that in each case the point is the same point C. Let the perpendicular bisectors of AB and AD intersect in the point F. The point F is equidistant from points A and B and also from points A and D. Therefore, the point F is also equidistant from points B and D. By definition this means that F is on the perpendicular bisector of BD. Also, we can conclude that the point F is the circumcenter C because it is the only intersection of the three perpendicular bisectors which means that it is equidistant from the three vertices.