Assignment #8

For EMAT 6680
Authored By

Kevin Adams

INTRODUCTION:

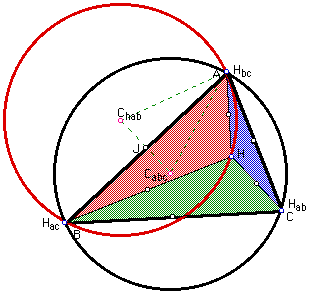
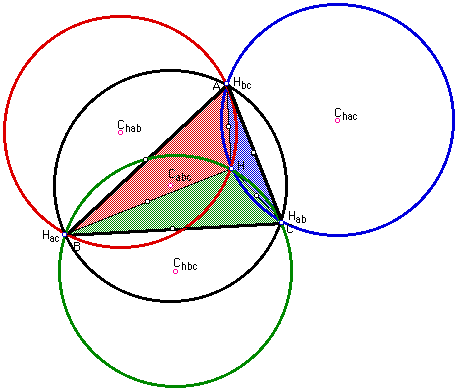
In this write-up we will take a look at a triangle ABC. First we will find the orthocenter, H, of this triangle. Then we will construct the triangles, HBC, HAB, and HAC along with their circumcenters and circumcircles. We will also construct the circumcenter and circumcircle for triangle ABC. The diagram of these constructions is pictured below. After constructing this it appears that the four circumcircles are all the same size. By same size, I mean that they appear to have the same area. Therefore, the hope of this write up is to prove this conjecture.

Before we being the proof we can use GSP to give us a measurement of the circles to give us an indication of whether or not the conjecture is true. Here are the results:

GREEN-Area(Circle C(hbc)H(ab)) = 53.258 square cm
BLACK-Area(Circle C(abc)H(ab)) = 53.258 square cm
BLUE-Area(Circle C(hac)H(bc)) = 53.258 square cm
RED-Area(Circle C(hab)H(ac)) = 53.258 square cm

PROOF:

To prove our conjecture it is sufficient to prove that the area of the black circle is equal to the area of any of the other three circles. Let us choose the red circle and prove that it's area is equal to the area of the black circle. It should be clear that the area of the green and blue circles could be proven equal in a similar fashion.

First note that the segment AB is a chord for both the black and red circles. Also, recall that the point Chab is the center of the red circle and the point Cabc is the center of the black circle. To prove that the two circles have equal area it is sufficient to show that the radius of each circle is equal. At this point we must recognize the fact that the centers Chab and Cabc are reflections of each other across the chord AB. Therefore, segment JChab is congruent to segment JCabc. Also, we know that segment ChabCabc is perpendicular to chord AB. Therefore angles AJChab and AJCabc are congruent. Also, AJ is congruent to itself. Therefore we have congruent triangles by SAS. Hence, AChab is congruent to ACabc. Since these two segments are also the radii of the chosen circles it remains that the two circles have equal areas and are thus congruent. Therefore, similarly, all four of the original triangles are congruent.

 

Return to Kevin's Main Page