

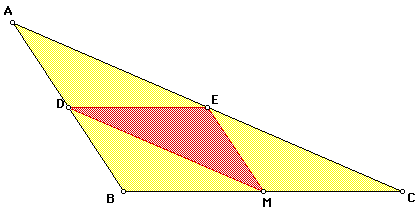
The medial triangle is formed by connecting the midpoints of the sides of the original triangle. Below, D MED is the medial triangle.
Here are two theorems and proofs concerning medial triangle:
1. The medial triangle is similar to the original triangle. PROOF
2. The medial triangle is one-fourth the area of the original triangle. PROOF
Take a look at the Euler segment and incenter of the medial triangle as it compares to the Euler segment of the original triangle:

The dashed Euler segment with the solid point labels are associated with the original triangle. The red Euler segment and outlined, primed (') labels are associated with the medial triangle. Observations:
1. The centroids (G' and G) of the medial triangle and original triangle are the same.
2. The Euler segment (H'C') of the orthic triangle shares a common endpoint with and lies on half of the Euler segment (HC) of the original triangle.That is, the Euler segment of the medial triangle (H'C') is one-half the length of the Euler segment of the original triangle (HC).
3. The orthocenter of the medial triangle (H') is the same as the circumcenter (C) of the original triangle. This is the common endpoint mentioned above.
4. The circumcenter of the medial triangle (C') is the midpoint of the Euler segment of the original triangle.
5. The incenter of the medial triangle (I'), incenter of the original triangle (I), and common centroid lie on the the same line. (Connect the incenters to visually verify this.)
The orthic triangle is formed by connecting the feet of the altitudes. Below, D ORT is the orthic triangle.
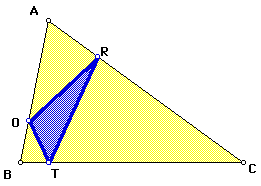
Notice that orthic triangle is not similar to the original triangle, nor is there any special relationship between the areas.
Take a look at the Euler segment and incenter of the orthic triangle as it compares to the Euler segment of the original triangle:
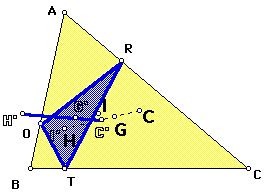
The dashed Euler segment with the solid point labels are associated with the original triangle. The solid purple Euler segment and outlined, primed (') labels are associated with the orthic triangle. Observations:
1. As long as the original triangle is acute, the incenter (I') of the orthic triangle and the orthocenter (H) of the original triangle are the same.
2. When the original triangle is right or obtuse, then the incenter (I') of the orthic triangle is the vertex of the obtuse angle of the original triangle. Also, when the triangle is a right triangle, the the orthic triangle is collapsed and has no area; i.e., it is only a segment.
3. While there is no relationship between the lengths of the Euler segments (H'C' and HC) of the two triangles, the circumcenter (C') of the orthic triangle lies on and is in fact the midpoint of the Euler segment (HC) of the original triangle as long as the original triangle is acute.
MIDSEGMENT TRIANGLE
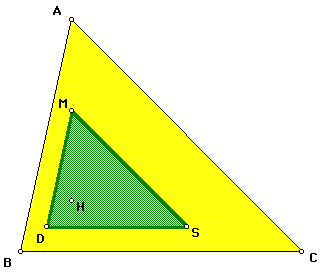
The midsegment triangle is formed by connecting the midpoint of each segment whose endpoints are a vertex of the original triangle and its orthocenter H.
Below, D MDS is the midsegment triangle.
Here are two theorems and proofs concerning midsegment triangle:
1. The midsegment triangle is similar to the original triangle. PROOF
2. The midsegment triangle is congruent to the medial triangle. PROOF
Take a look at the Euler segment and incenter of the midsegment triangle as it compares to the Euler segment of the original triangle:
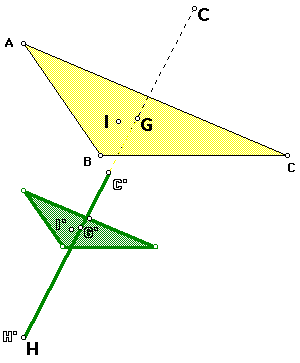
1. Both triangles share the same orthocenter (H and H').
2. The Euler segment (H'C') of the midsegment triangle lies on the Euler segment (HC) of the original triangle.
3. The circumcenter (C') of the midsegemnt triangle is the midpoint of the Euler segment (HC) of the original triangle. Therefore, the Euler segment (H'C') of the midsegment triangle is half the length of the Euler segment (HC) of the original triangle.
4. The centroid (G') of the midsegment triangle is the midpoint of HG (orthocenter to centroid) of the original triangle.
NINE POINT CIRCLE The nine point circle is a circle associated with a given triangle. nine points which lie on this circle are:
the three midpoints of the sides of the triangle,
the three feet of the altitudes, and
the three midpoints from the respective vertices to the orthocenter.
Note that these are the vertices of the medial, orthic, and midsegment triangles, respectively of the original triangle.
Since the vertices of these three secondary triangles lie on the nine-point circle, then the nine-point circle must be the common circumcircle of the three secondary triangles.
This is verified by the fact that each of the three circumcenters (C') of the secondary triangle is the midpoint of the Euler segment (HC) of the original triangle; therefore, the secondary triangles share the same circumcenter (C'), and thus the same circumcircle. This circumcenter is the center of the nine-point circle.
Here is a picture that you can manipulate.
original triangle: D ABC
medial triangle: D MED
orthic triangle: D ORT
midsegment triangle: D M'D'S
nine-point circle (center N or C'): C' is the common circumcenter of the secondary triangles.