

A few facts about the medians of a triangle:
1. Each median divides the triangle in half.
2. The three medians are concurrent at a point called the centroid.
3. The centroid is two-thirds the distance from a vertex to the midpoint of the side opposite that vertex.
GSP Verification (for 2 and 3)
PROOF (for 2 and 3)
Here is a picture of a triangle, its medians, centroid (G), and triangle of medians using the lengths of the medians. Notice that I used one of the medians (segment Aa) as one of the sides of the triangle of medians. This causes the triangle of medians to overlap with the original triangle.
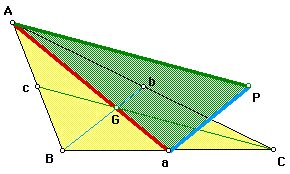
How might we construct the triangle of medians? How do I make sure that AP = cC and aP = Bb?
The general idea is to use one of the medians as one of the sides of your triangle of medians.
By constructing a line through point a that is parallel to segment Bb and a line through point b that is parallel to side BC, you can create a parallelogram BbPa where aP = Bb.
Similarly, by constructing a line through point A that is parallel to segment cC and a line through point C that is parallel to side AB, you can construct parallelogram AcCP where AP = cC.
If you would like to see these lines used to construct the triangle of medians, double-click on the Construction lines button in the sketch.
The triangle of medians does not appear to be congruent or similar to the original triangle. However, it is worthwhile to compare the areas and perimeters. According to the measurements, it seems that there is no constant ratio of the perimeters. However, the ratio of the areas is a constant. In fact, the calculation reveals that the area of the triangle of medians is three-fourths the area of the original triangle!
Let's prove it:
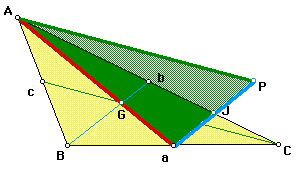
First of all, notice how part of the triangle of medians overlaps a part of the original triangle. In fact, it overlaps a certain fraction of the original triangle. Recall that median Aa divides the triangle's area in half. Notice that D AaJ lies on most of D AaC, which is half the area of the original triangle. How much of that half of the triangle is it???
Perhaps it would be easier to consider the "leftover" part, D CJa. Recall that segment aJ || segment Bb. Therefore, D CJa ~ D CbB. D CbB is created by a median; therefore, the area of D CbB is half the area of the original triangle. Since point a is the midpoint of side BC, then the sides and height of D CJa are half the length of the sides and height of D CbB.
So,
Area of D CJa = (1/2)* [ (half of base of D CbB)*(half of height of D CbB) ]
= (1/2)* [ (1/4)*(base of D CbB)*(height of D CbB) ]
= (1/4)* [ (1/2)*(base of D CbB)*(height of D CbB) ]
= (1/4)*(area of D CbB)
= (1/4)*(area of D AaC) since D AaC is also created by a median and is therefore 1/2 the area of the original triangle.
Since (area of D CJa) + (area of D AaJ) = (area of D AaC), then D AaJ must be 3/4 the area of D AaC. Since the area of D AaC is already 1/2 the area of the original triangle, then D AaJ is (3/4) of (1/2) of the area of the original triangle. That is, D AaJ is 3/8 the area of the original triangle.
Is D AaJ half the area of the triangle of medians? If it is, then that would mean that the rest of the triangle of medians, D AJP, is also 3/8 the area of the original triangle. Therefore, the entire triangle of medians would be (3/8 + 3/8) = 6/8 = 3/4 the area of the original triangle.
Consider this picture:
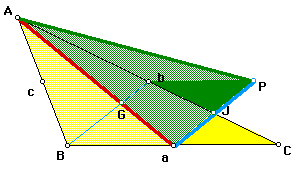
Segment bP || segment BC (segment bP is part of the line parallel to side BC). Therefore,
m< JaC = m< JPb (alternate interior angles)
m< CJa = m< bJP (vertical angles).
Also, bP = Ba (opposite sides of a parallelogram are congruent) and Ba = ac (since a is the midpoint of BC)
Therefore, bP = ac.
D JaC is congruent to D JPb (ASA Congruence). So Ja = JP.
This means that point J is the midpoint of side aP of the triangle of medians. Segment AJ is a median that divides the area of the triangle of medians in half. Therefore,
the area of the triangle of medians
= (the area of D AaJ) + (the area of D AJP)
= (3/8 the area of D ABC) + (3/8 the area of D ABC)
= 3/4 the area of D ABC.