

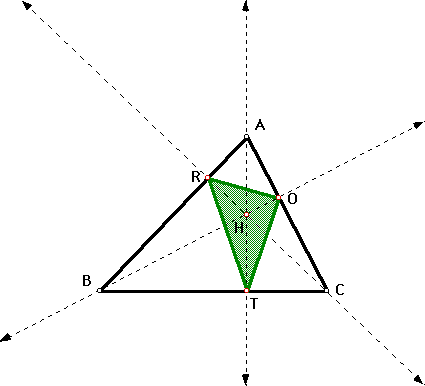
An altitude in a triangle is a perpendicular segment from a vertex to the side opposite that vertex. Below, the three altitudes of D ABC are extended. Also, the intersection points (feet) of the altitudes and the sides of the triangle are labeled O, R, and T. The segments connecting these feet of the altitudes form the orthic triangle, D ORT. Point H is the orthocenter of D ABC.
Recall that the circumcircle of D ABC is a circle "around" the triangle. That is, the vertices of D ABC lie on the circumcircle. Below is a picture of the circumcircle of D ABC. The points of intersection of the circumcircle and altitudes are marked X, Y, and Z. These points are connected to form D XYZ. We will refer to this triangle as the circum-altitude triangle (If anyone knows the official name of it, feel free to let me know!!!).
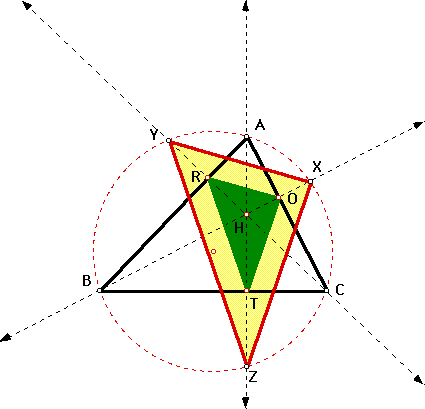
You probably have a suspicion that D XYZ and D ORT have some relationships. For example, they appear to be similar.
Here are a few observations that can be made. Click on the picture to investigate and verify these conjectures in GSP:
1. The orthic triangle (D ORT) and circum-altitude triangle (D XYZ) are similar.
PROOF
2. The area of the orthic triangle (D ORT) is one-fourth the area of the circum-altitude triangle (D XYZ).
PROOF
3. The perimeter of the orthic triangle (D ORT) is one-half the perimeter of the circum-altitude triangle (D XYZ).
PROOF
4. The orthic triangle (D ORT) and circum-altitude triangle (D XYZ) have the same incenter.
PROOF
5. The incenter of the orthic (D ORT) and circum-altitude (D XYZ) triangles is the orthocenter of the original triangle.
PROOF