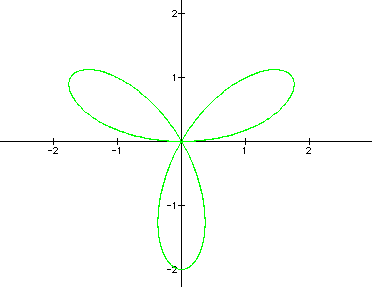
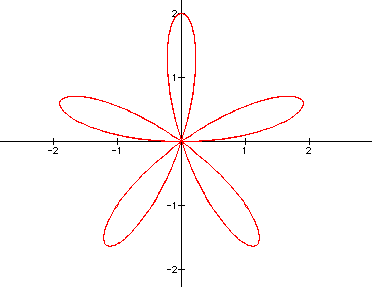
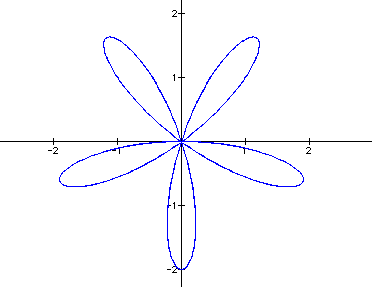
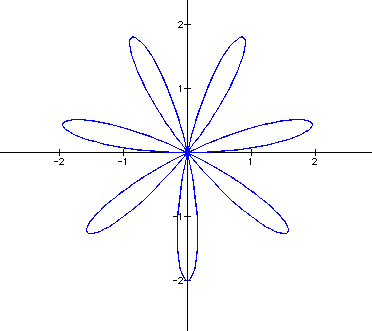
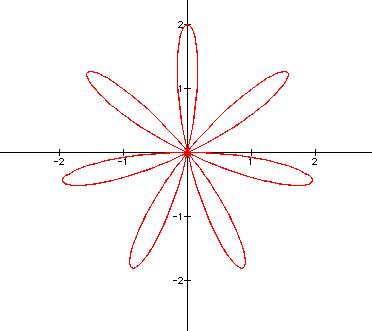
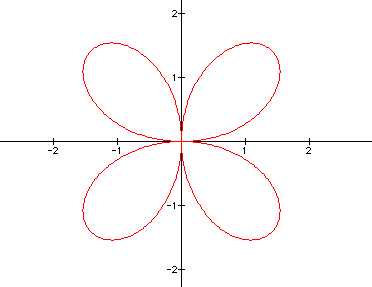
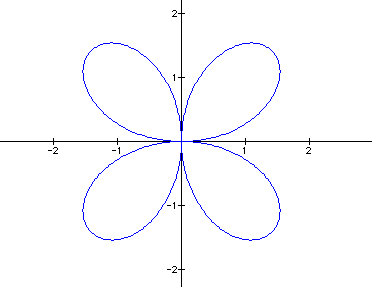
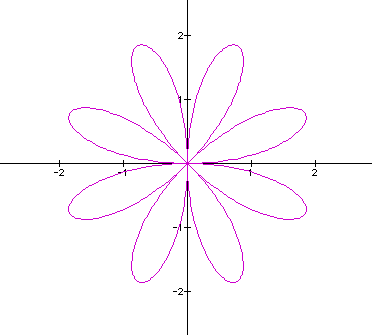
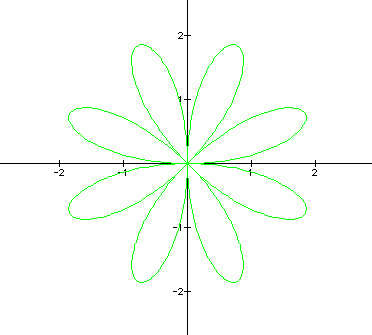
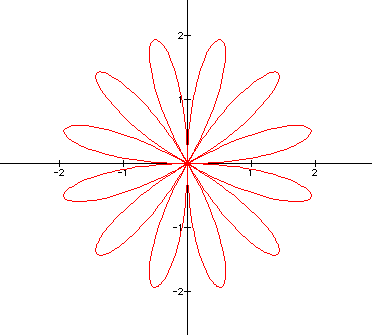
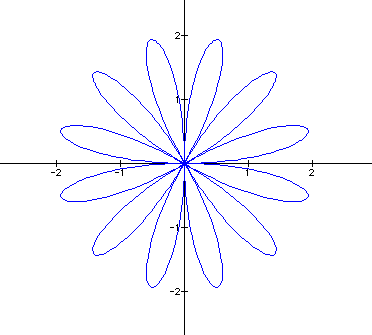
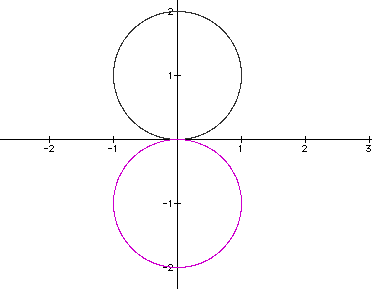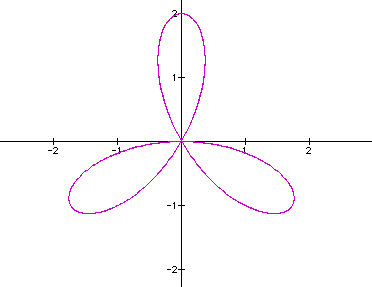The graphs of the equation are known as roses with various numbers of leaves. Below are graphs of the above equation with a = 1 and varied values for k. It appears that k affects the number of "petals" of the graph. If k is odd, then there are k petals. If k is even, then there are 2k petals. A negative value for k reflects the graph about the x-axis.
ODD k graphs ( k = 1, 3, 5, 7)
EVEN k graphs ( k = 2, 4, 6 )
Notice that when k is odd, there is always one petal that "lies" on the y-axis in such a way that the y-axis goes through the center of the leaf (as if it were a vein through the center of the leaf). We will call this petal the "axis petal."
When k = 1, 5, 9, 13, ..., the axis petal is on the positive y-axis. Notice that these are the odd numbers which are congruent to 1 modulo 4.
When k = 3, 7, 11, 15, ..., the axis petal is on the negative y-axis. Notice that these are the odd numbers which are congruent to 3 modulo 4.
Glance at the the graphs to verify these conclusions.
Then go on to "What
does a do?"