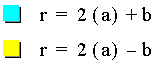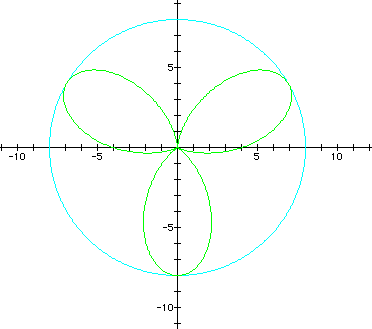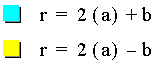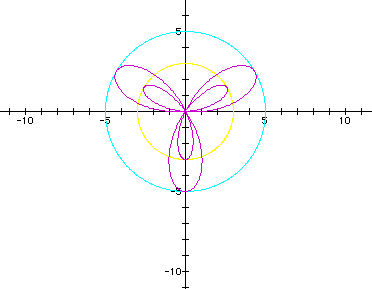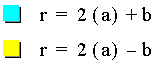![]()
![]()
![]()
![]()
![]()
![]()
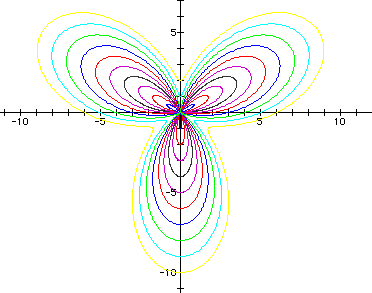
Make the following observations about the graphs
of the equation when k is odd and the go on to investigate
graphs of this equation when "k is even."
Since k is odd, there are k petals with a petal lying on the y-axis. Review when this axis petal lies on the positive or negative y-axis. We can classify the graphs into three groups:
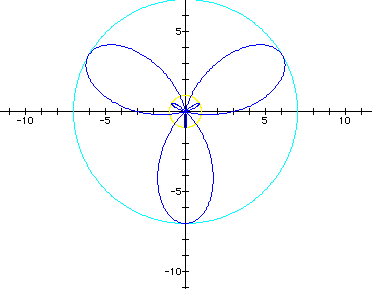
1. Single roses with closed petals that converge at the origin. This occurs when b = 0 and when b = 2a. The radius of the rose is given by r = 2a + b.
(graphs in black and green).
2. Double roses composed of outer and inner petals. This occurs when b < 2a. There are two radii to consider: the radius of the (1) outer rose is given by r = 2a + b. (2) the inner rose is given by r = 2a - b.
(graphs in purple, red, and blue)
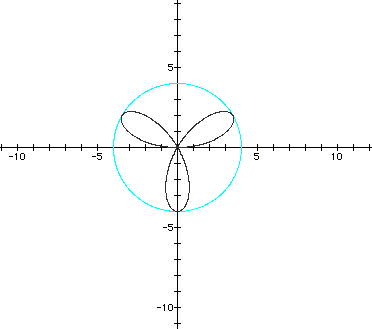
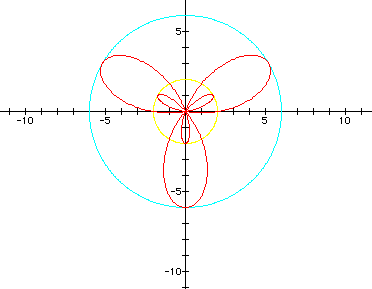
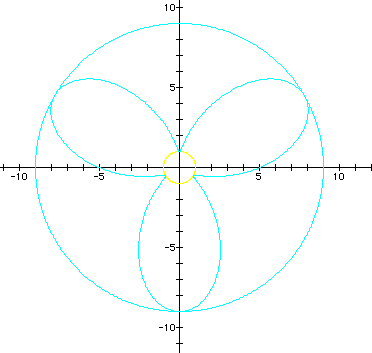
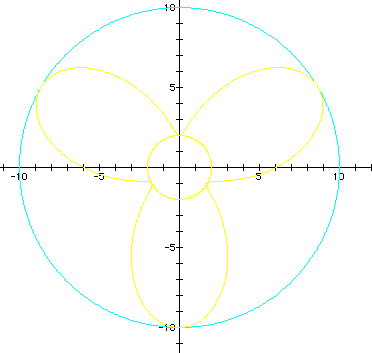
3. Open-petaled roses with an opening or core in the center. This occurs when b > 2a. There are two radii to consider: the radius of the (1) rose is given by r = 2a + b. (2) the core is given by r = 2a - b.
(graphs in cyan and yellow)
NOTE: The graphs of the equations with negative values of b look the same. Perhaps they are simply reflections about the y-axis. In cases where the radius was r = 2a + b in a positive b graph, the radius for a negative b graph has a radius of r = 2a - b. And in cases where the radius was r = 2a - b in a positive b graph, the radius for a negative b graph has a rdius of r = 2a + b.
Also, recall that if a or k (but not both) is negative, the graph is reflected about the x-axis. If BOTH a and k are negative, then the graph is the same as if both were positive.