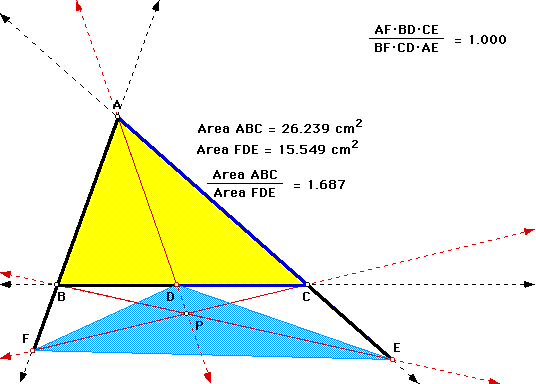
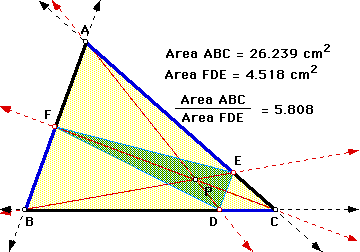
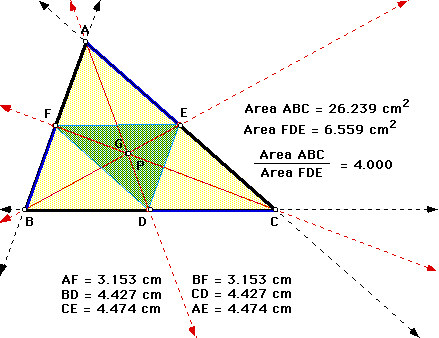
A. Conjecture
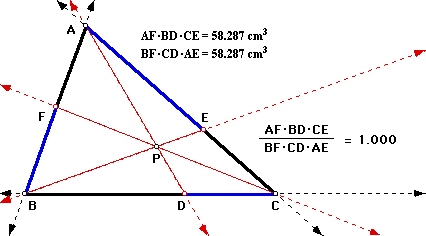
The products (AF)(BD)(EC) and (FB)(DC)(EA) are equal for all types of triangles and locations of P. Click on the picture to explore various types of triangles and locations of P. Note that the sides of the triangle are extended, allowing you to investigate when P is outside the triangle. The products are also equal when P is outside the triangle.
B. Proof
The plan for the proof is to create parallel lines to produce similar triangles which involve the segments in the products. We will then use ratios of proportional parts of these triangles to prove that the products are equal.
First, construct lines through B and C which are both parallel to line AP.
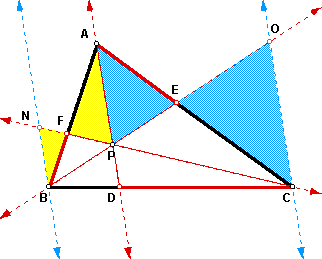
Let N be the point of intersection of line CP and the line parallel to line AP through B. Let O be the point of intersection of line BP and the line parallel to line AP through C. So, BN || AP || CO. Notice the pairs of similar triangles:
D AFP ~ D BFN (AA Similarity) since
m< AFP = m< BFN (vertical angles);
m< FAP = m< FBN (BN || AP; AB is a transversal; alternate interior angles).
Therefore,
(1)
.
D AEP ~ D CEO (AA Similarity) since
m< AEP = m< CEO (vertical angles);
m< EAP = m< ECO (AP || CO; AC is a transversal; alternate interior angles).
Therefore,
(2)
Also,
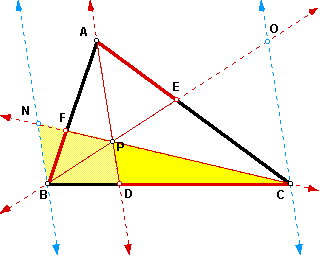
using BN || AP:
D CDP ~ D CBN (AA Similarity) since
m< DCP = m< BCN (shared angle);
m< CDP = m< CBN (BN || AP; BC is a transversal; corresponding angles).
Therefore,
(3)
And
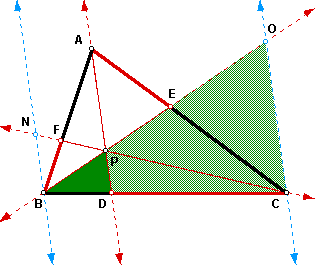
using AP || CO:
D BDP ~ D BCO (AA Similarity) since
m< DBP = m< CBO (shared angle);
m< BDP = m< BCO (AP || CO; BC is a transversal; corresponding angles).
Therefore,
(4)
.
Now the task is to use the ratios in (1) - (4) to get our desired result:
We must be strategic in selecting our ratios. We need to use ratios that involve terms that are in our desired result as well as common terms that might "cancel out" when we multiply. Therefore, from the above ratios we need the following:
(1) (2) (3) (4)
Notice that we used some reciprocals in (2) and (3) in anticipation of what is next.
Let's multiply the ratios in the order (1)(4)(2)(3):
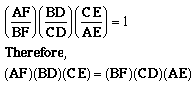 .
.C. GSP Sketch to manipulate the following pictures.