

Given D ABC, let points D, E, and F be midpoints of the sides BC, AC, and AB, which are opposite < BAC, < ABC, and < ACB, respectively. The medians are the segments AD, BE, and CF, whose endpoints are a vertex and the midpoint of the side opposite that vertex. The general idea of this proof is to choose one of the medians, such as AD. Then show where a second median BE intersects median AD. Next, we will show where the third median CF intersects median AD. If the intersection point of median AD and median BE is the same intersection point of median AD and median CF, then it follows that the three medians are concurrent.
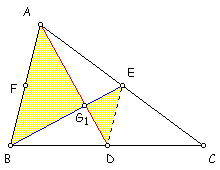
Here we have D ABC with medians AD and BE drawn
with an intersection point G1. Also, we have connected
the midpoints of sides AC and BC to get segment
DE. Recall that a segment DE is parallel to side
AB and is one-half the length of side AB. (Midsegment
Theorem) Since DE || AB then it follows that
m< BAG1 = m< EDG1 (alternate interior angles)
m< ABG1 = m< DEG1 (alternate interior angles)
m< AG1B = m< DG1E (vertical angles).
Therefore, D ABG1 ~ D DG1B.
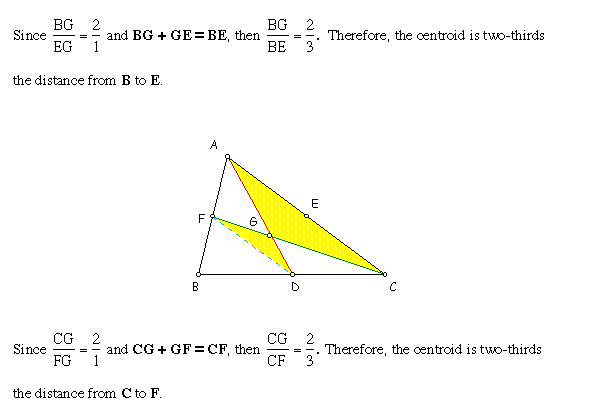
Recall that
Therefore, the scale factor for the triangles must also be 2:1.
That means that
![]()
In other words, the distance from the
vertex A to the point G1 where the two medians intersect is TWO-THIRDS
the distance from the vertex A to the midpoint D
of the opposite side BC.
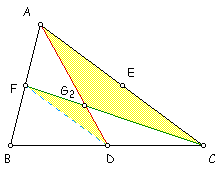
Here we have D ABC with medians AD and CF drawn with an intersection point G2. Also, we have connected the midpoints of sides AB and BC to get segment DF.

In other words, the distance from the vertex A to the point
G where the two medians intersect is TWO-THIRDS
the distance from the vertex A to the midpoint D
of the opposite side BC.
Since both medians BE and CF intersect median AD
at a point that is TWO-THIRDS the distance from
vertex A to the midpoint of the opposite side BC,
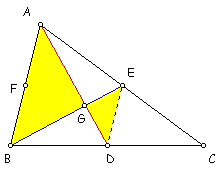
then it follows that G1 = G2.
So the three medians must be concurrent
at a point. We call this point the centroid and label it
G. If a triangle were a uniform object cut from sheet of
materiel, it would act as the center of gravity for the triangle.
That is, one could balance the triangle with its centroid placed
on the tip of a pencil.
To prove that the centroid is two-thirds the distance from any vertex to the midpoint of the side opposite that vertex, you simply use the two sets of similar triangles that were formed above and the fact that the scale factor is 2:1. We can now replace G1 and G2 with G since we proved that G1 = G2.
The same argument holds for an obtuse triangle.
The same argument holds for a right triangle.
Notice that for any triangle, the centroid lies inside the triangle since it is a point that lies on all medians.