

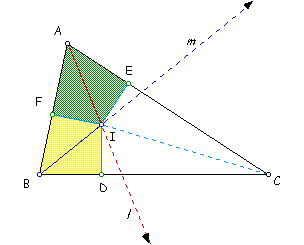
Let D ABC be an acute triangle. Let l be the line which contains the angle bisector of < BAC. Let m be the angle bisector of < ABC. Let point I be the point of intersection of l and m.
Since I lies on the angle bisector of < BAC, I is equidistant from the sides (AB and AC) of < BAC. (Angle Bisector Theorem) Let IF and IE be perpendicular segments from I to the sides AB and AC, respectively. Then, IF = IE.
Since I lies on the angle bisector of < ABC, I is equidistant from the sides (AB and BC) of < ABC. (Angle Bisector Theorem)
Let IF and ID be perpendicular segments from I to the sides AB and BC, respectively. Then, IF = ID.
Since IE = IF and IF = ID, then IE = ID. (Transitive Property) Therefore, I is equidistant to the sides (BC and AC) of < ACB. I must also lie on the angle bisector of < ACB. (Converse of the Angle Bisector Theorem) Therefore, the three angle bisectors are concurrent at a point I equidistant from the three sides. This point is called the incenter. The incenter is the center of the inscribed circle of D ABC.

Let D ABC be an obtuse triangle with < ABC
as an obtuse angle. All the conditions in the proof for an acute
triangle hold for an obtuse triangle.
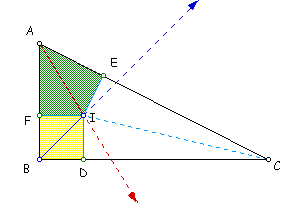
Let D ABC be a right triangle
with < ABC as a right angle. All the conditions in the
proof for an acute triangle hold for an obtuse triangle. Additionally,
notice that ID || AB since both AB and ID
are perpendicular to BC. Also, IF || BC since both
BC and IF are perpendicular to AB.
The incenter is always located inside a triangle since it lies within the interior of each of the three angles.