

Given D ABC, let lines l and m be the lines through vertices A and B be perpendicular to the opposite sides BC and AC, respectively. Let H be the point of intersection of l and m. This proof involves using the coordinate plane to show that H also lies on the line through C perpendicular to its opposite side AB. Recall the following facts about the coordinate plane:
(1) The slope of a line can be calculated using two points (a, b) and (c, d) on the line.
(2) The slopes of perpendicular lines are negative reciprocals of each other.
(3) The point-slope form of the equation of a line is y - y1 = m(x - x1) where
(x1 , y1) is a point on the line and m is the slope of the line.
(4) The slope-intercept form of the equation of a line is y = mx + b where m is the
slope of the line and b is the y-intercept.
Let the vertices have the following coordinates: A (b,
c); B (0, 0); C (a, 0).
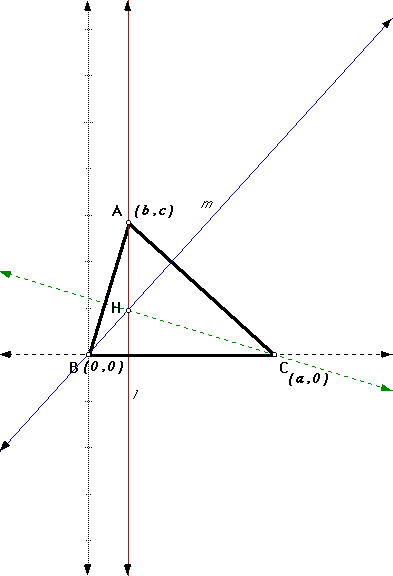
The slope of the line containing BC is
Therefore, the slope of the line perpendicular to line BC through A at (b, c) is undefined. The equation of the perpendicular line is x = b. The slope of the line containing AC is
Therefore, the slope of the line perpendicular to line AC through B at (0, 0) is
The equation of the perpendicular line is
The slope of the line containing AB is
Therefore, the slope of the line perpendicular to line AB through C at (a, 0) is -(b/c). The equation of the perpendicular line is
This information is summarized in the following chart:

To find the coordinates of H, the intersection point of lines l and m, simply solve the system of equations of these two lines:
The y-coordinate can be found by substituting
for x:
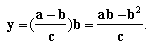
Therefore, the coordinates of H are
To determine if the line containing the altitude from C to AB, substitute the coordinates for H into the equation
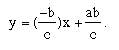
.
This implies that H does in fact also
lie on the line containing the third altitude of the triangle.
Therefore, the three altitudes of the triangle are concurrent
at point H. This point is called the orthocenter
and is labeled as H.
This proof holds for obtuse and right triangles
(See figures below) as well. Notice that if the triangle
is obtuse, the orthocenter lies outside the triangle. If the triangle
is right, the orthocenter is the vertex of the right angle since
the two sides that form the right angle lie on two altitudes.