

Heron (also known as Hero) of Alexandria (fl.
A.D. 62) lived sometime between 100 B.C. and A.D. 100. Heron was
a Greek geometer, surveyor, and inventor who taught computational
geometry, arithmetic geodesy, physics, mechanics, and pneumatics
(theory and use of air pressure) at the Museum. Known as a rather
clever inventor, some of Heron's possible inventions include an
improved dioptra for surveyors, a screw cutter, a simple steam
engine (aeolipile), and war engines.
Heron's works exhibit a mixture of rigorous
mathematics and approximate procedures and formulas of the Egyptians.
He was also concerned with applied geometry and mechanics. His
works include Metrica, Geometrica, Geodesy (all give theorems
and rules for plane areas, surface areas, and volumes of several
figures), and Dioptra (a book on land surveying).
His applied works include Mechanics, The Construction of
Catapults, Measurements, The Design of Guns, Pneumatica, On the
Art of Construction of Automata. He gives designs for water
clocks, measuring instruments, automatic machines, weight-lifting
machines, and war engines.
Heron is most famous for his formula for the area of a triangle:
where a, b, and c are the lengths of the triangle's sides and s is the semiperimeter:
Heron's proof relies on the basics of Euclidian
geometry. However, the proof seems to be random. It involves a
seemingly endless path of relationships, similarity, and ratios
that finally come together to make a proof. Heron begins with
some preliminary results. The first two come from Euclid.
PROPOSITION 1
The bisectors of the angles of a triangle meet at a point that
is the center of the triangle's inscribed circle. This point is
known as the incenter. (In the figure, point I is the incenter.
The r is the radius of the incircle.)
This is Proposition IV.4 of Euclid's Elements.
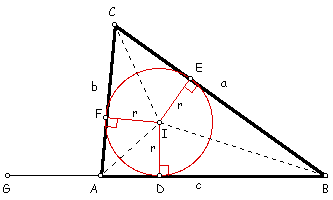
PROPOSITION 2
In a right triangle, if a perpendicular is drawn from the right
angle to the base, the triangles on each side of it are similar
to the whole triangle and to each other. (In the figure ,
D
APC ~ D BPA ~ D BAC.)
This is Proposition VI.8 of Euclid's Elements.
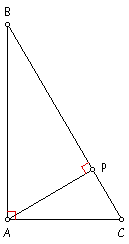
PROPOSITION 3 In a right triangle, the midpoint of the hypotenuse is equidistant from the three vertices. (In figure, AM = BM = CM.) This theorem appeared nowhere in Euclid's Elements.

PROPOSITION 4 If AHBI is a quadrilateral with diagonals AB and IH, and if < HAB and < HIB are right angles, then a circle can be drawn passing through the vertices A, I B, and H. AHBI is called a cyclic quadrilateral.
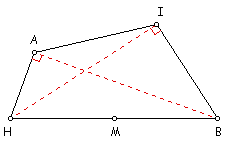
PROPOSITION 5 The opposite angles of a cyclic quadrilateral
sum to two right angles.
This is Proposition III.22 of Euclid's Elements.
While these propositions seem irrelevant, they
are what Heron used. Here is the proof that Heron used:
PART A
Heron began by inscribing a circle
within the triangle. In the figure, ID = IE = IF = r.


This gives us a link between the triangle's
area and semiperimeter.
PART B
In the figure below, the angles
of D
ABC are bisected and ID = IE = IF.

Since ID, IE, and IF are perpendicular to the sides of the D ABC, then three pairs of congruent right triangles are created:

Heron's segment BG = s. Thus,
BG is a pictorial representation of the semiperimeter.
Apparently, Heron wanted to have a line segment as a representative
of the semiperimeter as a part of the picture. The following are
then derived:
(1) s c = BG AB
s c = AG.(2) s b = BG AC
= (BD + AD + AG) (AF + CF)
= (BD + AD + CE) (AD + CE)
s b = BD.
since AD = AF and AG = CE = CF. Likewise,(3) s a = BG BC
= (BD + AD + AG) (BE + CE)
= (BD + AD + CE) (BD + CE)
s a = AD
since BD = BE and AG = CE.
As a result, the semiperimeter s, as
well as the quantities (s a), (s b), and
(s - c) all appear as segments in the diagram.
PART C
Now Heron was left with the task of
linking these facts in such a way to complete his argument. The
figure below illustrates Heron's next line of reasoning.
Heron constructed a line perpendicular to AB through
point A and a line perpendicular to IB through point
I. This line intersects AB at point K. The two
lines constructed intersect at point H. Segment BH
is constructed.
The result is quadrilateral AHBI. This is the same type
of cyclic quadrilateral mentioned in Proposition 4. Therefore,
by Proposition 5, its opposite angles sum to two right angles.
Therefore,
< AHB + < AIB = 2 right angles.
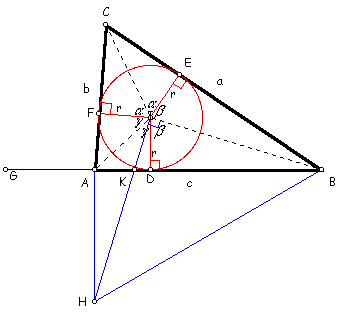
Now focus on the angles created by the angle bisectors and segments
ID, IE, and IF. By the congruences from part
B, we get three pairs of congruent angles, so that
2a + 2b + 2g = 4 right angles = 360 degrees
so
a + b + g = 2 right angles = 180 degrees.Since (b + g) = m< AIB, then
a + < AIB = 2 right angles = < AHB + < AIB.
This seems rather insignificant, but will prove to be crucial to what Heron did next.




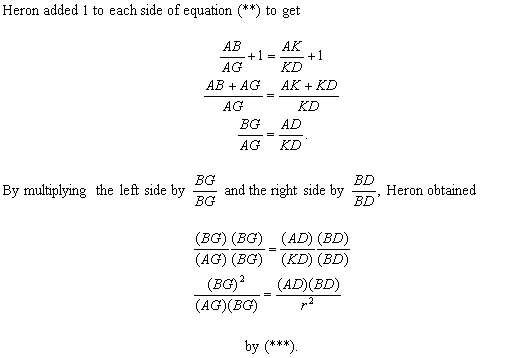
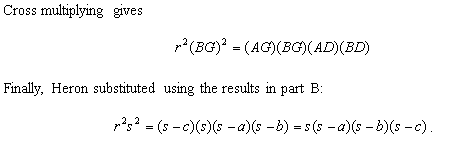
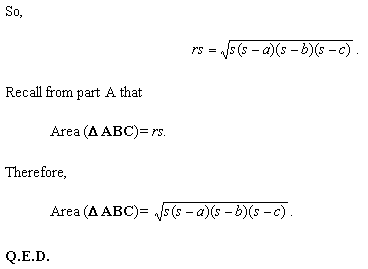
While Heron's proof uses elementary geometry,
it is quite intricate. It is hard to imagine how he must have
arrived at the directions that he chose to take! One fact of interest
is that an old Arabic manuscript written by Islamic scholar Abu'l
Raihan Muhammed al-Biruni centuries after Heron credits this result
to Archimedes. However, there are no Archimedean writings to support
this claim.
Classics of Mathematics (Ronald Callinger)
Mathematical Thought from Ancient to ModernTimes (Morris Kline)
Journey Through Genius
Britannica.com