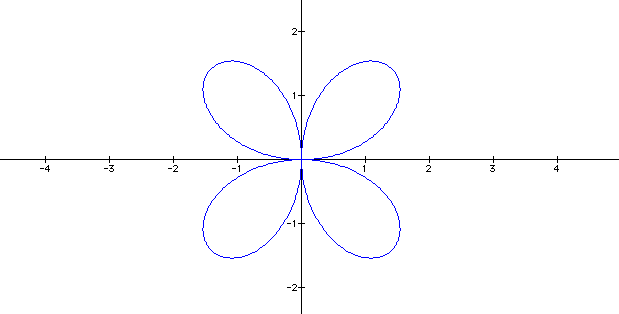This write up is for problems #2 in Assignment
11.
Investiagting Polar
Equations
by
Kimberly Burrell
and Brad Simmons
Investigation of
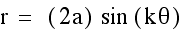 When a = 1 and k = 1, the polar equation
will produce the following graph.
When a = 1 and k = 1, the polar equation
will produce the following graph.
 At this point we can observe that the
circular shape has a center at 1 on the polar scale. The sine
equation is symmetric about the y-axis. If we first allow "a"
to vary we can observe some of the following situations.
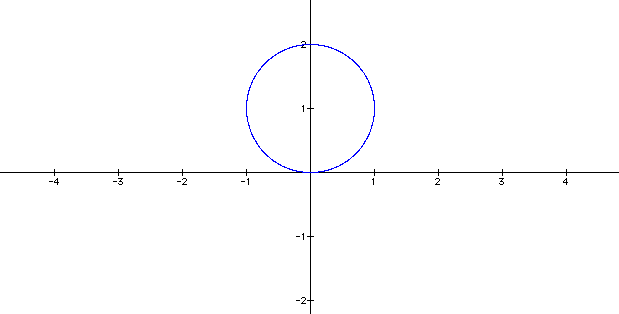
When a = 3 and k = 1, the circular
graph has expanded.
At this point we can observe that the
circular shape has a center at 1 on the polar scale. The sine
equation is symmetric about the y-axis. If we first allow "a"
to vary we can observe some of the following situations.
When a = 3 and k = 1, the circular
graph has expanded.
 The circular graph is now located between
0 and 6. Since "a" is multiplied by 2, then the graph
is expanding by 2 each time.
Now, we will vary "k" and
hold "a" constant at 1.
When k > 1, the graph no longer
has a circular shape. It now begins to appear to have pedals.
Such as the following graph where k = 2.
The circular graph is now located between
0 and 6. Since "a" is multiplied by 2, then the graph
is expanding by 2 each time.
Now, we will vary "k" and
hold "a" constant at 1.
When k > 1, the graph no longer
has a circular shape. It now begins to appear to have pedals.
Such as the following graph where k = 2.
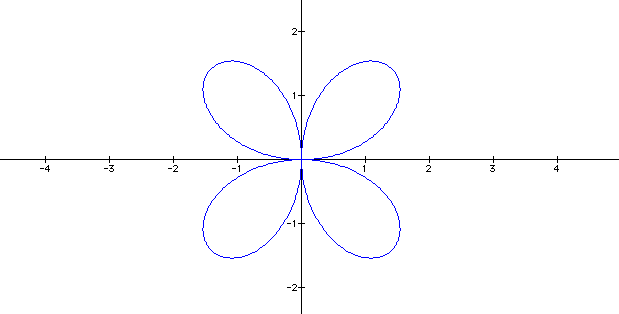 We notice that the graph has 4 pedal-like
curves. Can we conjecture that the number of pedals is k times
2? When k = 5, the graph does not have double the number of pedals,
but it only has 5 pedal-like curves.
We notice that the graph has 4 pedal-like
curves. Can we conjecture that the number of pedals is k times
2? When k = 5, the graph does not have double the number of pedals,
but it only has 5 pedal-like curves.
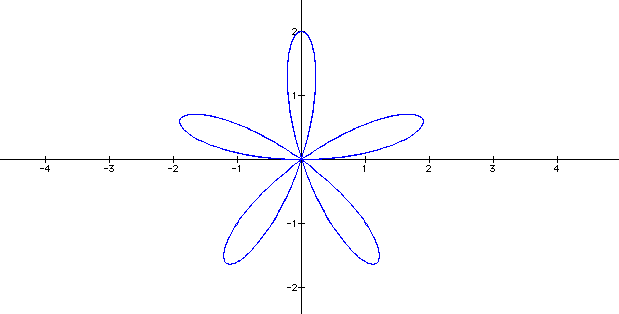 Therefore, one can observe that when
k is an odd number, the number of pedals will be equal to k. However,
when k is an even number, the number of pedals will be 2 times
k.
Finally, we will vary both "a"
and "k".
When a = 2 and k = 5, we would expect
the graph to have 5 pedals and to be expanded more than the graph
above. (See graph below)
Therefore, one can observe that when
k is an odd number, the number of pedals will be equal to k. However,
when k is an even number, the number of pedals will be 2 times
k.
Finally, we will vary both "a"
and "k".
When a = 2 and k = 5, we would expect
the graph to have 5 pedals and to be expanded more than the graph
above. (See graph below)
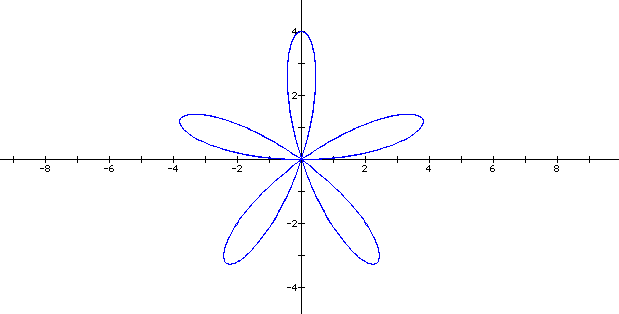 We were correct. There are 5 pedals
and the graph has been expanded from a magnitude of 2 to 4.
We were correct. There are 5 pedals
and the graph has been expanded from a magnitude of 2 to 4.
Return