This write up is for problems #2 in Assignment 11.

Investiagting Polar Equations

by

Kimberly Burrell and Brad Simmons

Investigation of

After we investigated the polar equation by varying "a" and "k", we were given a similar polar equation except for the addition of "b". At this point in our investigation, we will vary the "b" using the before mentioned values for "a" and "k". Again the cosine equation will remain symmetric about the x-axis.

We will now work with the cosine problem (red) which will be graphed over the sine problem (blue).

When all values are 1, we have the following graph.

The graph now has a distinct shape. There appears to be a smaller curve inside the larger curve and passing throught the origin. The cosine graph still appears to be rotated to the right. Will the curve behave like the previous curves if we change the value of "b" to 2? Let's see.

The smaller curve appears to disappear. However, there is still a noticable bend at the origin of the graph. The cosine graph (red) appears to have rotated to the right as before.

Now, let us vary both "k" and "b".

When a = 1, k = 2, and b = 2, we get the following graph.

Here, we can observe two petal-like curves that are connected at the origin with the cosine being rotated to the right.

Now let us change "a" to 2, also.

When a = 2, we get 4 petal-like curves that are connected at the origin. Two of these petals are smaller than the original two petals. Again, the cosine graph is rotated to the right. Now let us see what occurs when we change a = 5.

The pedals have expanded as with the previous changes of "a", and there was a rotation to the right. Therefore, if we change "k" the number of petals should change if the same principles for "k" apply in this polar equation.

Let us try k = 5.

By observation one can see that there are 5 large petals and 5 small petals which are inside the larger ones.

Finally, we will let all values of a, k, and b vary.

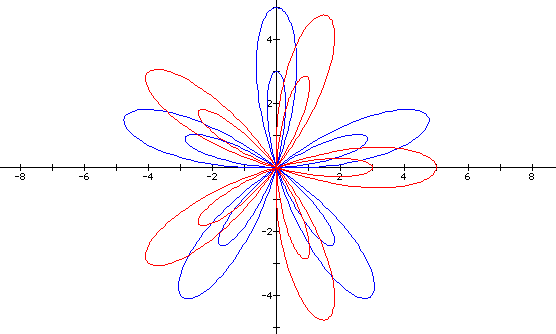
Here a = 2, b = 1, and k = 5. What conclusions can you draw from this?

Return