Proof that the Golden Ratio is Approached by the Ratio of Adjacent Terms of the Fibonnaci Sequence

by

Kimberly Burrell

Recall that the Fibonnaci Sequence is the sequence described by f(0)=1, f(1)=1, with f(n)=f(n-1) + f(n-2). In particular, we are interested in the ratio f(n+1)/f(n). We will call the ratio

.

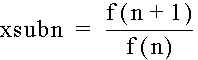We can assume that the limit of x sub n as n approaches infinity is x.

Thus,

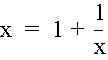
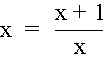
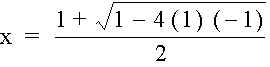or .

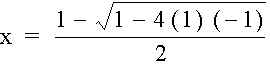Since, we are dealing with only the positive values of x,

,

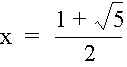which equals the Golden Ratio 1.618033988738303.

Return