

Assignment #6
Investigations of a Triangle formed by the Median
Lengths of Another Triangle
by
Kimberly Burrell
Given triangle ABC with medians AD, BE, and CF, we can construct a triangle in which the three sides have the lengths AD, BE, and CF. At this time we want to investigate the relationship between the original triangle and the new one.
After constructing these two triangles, we find the perimeter and area of each. We can then calculate the ratio of the triangle formed by the medians and the original triangle with respect to both perimeter and area.
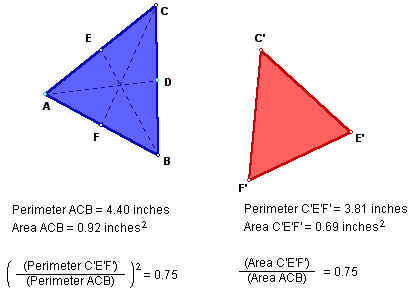
Notice that the ratio of the perimeters is not included, however we see the ratio of the perimeters squared. Comparing this particular ratio to the ratio of areas, we are able to find an equal ratio. Will this relationship be consistant with any triangle? Click here to try.
You will notice that as you manipulate the original triangle, the ratio of the area remains constant at 0.75. Can you find a case where the ratio of the perimeters squared is not 0.75? The question to explore and investigate now becomes when is the ratio of the perimeters squared not 0.75?