

Pedagogical Value to the concept of
Tangent Circles
The current high school mathematics curriculum calls for students to study and comprehend the underlying principles of conic sections including ellipses and hyperbolas. As we have seen, the locus of the center of the tangent circle to two given circles is either an ellipse or a hyperbola, depending on the placement of the given circles.
The Ellipse
To begin to teach students about ellipses, we start off with a discussion of the following picture, in which F1 and F2 are the foci of the ellipse and P is any point on the ellipse.
P*F1 + P*F2 = k where k is some constant.
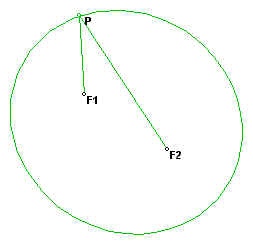
It is also important for students to have a deeper understanding of how to generate the above illustration and why the equation is true. The construction of a circle tangent to two given circles clearly demonstrates both of these concepts.

Here one can see that F1 is the center of one of the given circles and F2 is the center of the other given circle. P is again any point on the ellipse, and is also the center of the tangent circle.
The Hyperbola
To begin to teach students about hyperbolas, we start off with a discussion of the following picture in which F1 and F2 are the foci of the hyperbola and P is any point on the hyperbola.
P*F1 - P*F2 = k where k is some constant. Click here to see the picture.
Here one can observe that F1 is the center of one of the given circles and F2 is the center of the other given circle. P is again any point on the hyperbola, and is also the center of the tangent circle.