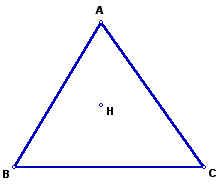
To begin our investigation , we will construct the orthocenter (H) of triangle ABC. An orthocenter is the common intersection of the three altitudes of a triangle. An altitude is a line which is drawn from a vertex perpendicular to the opposite side.
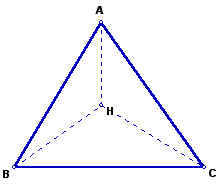
By using the orthocenter (H) as a vertex point, we can construct three triangles inside our original triangle.
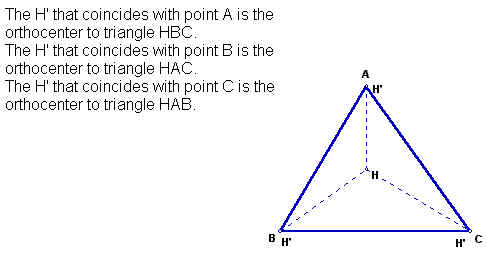
We now can construct the orthocenter (H') of each triangle. Notice that H' coincides with a vertex of the original triangle.
Now. let's look at triangles ABC, HAB, HAC, and HBC and their circumcircles.
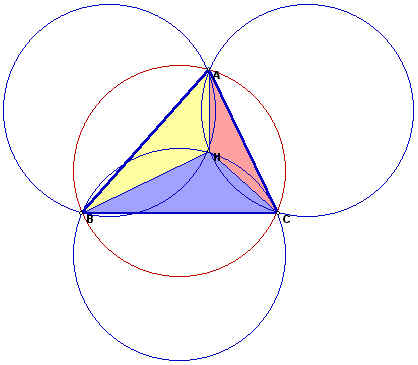
The red circle is the circumcircle of triangle ABC, and the three blue circles are the circumcircles of the other triangles.
One interesting conjecture is that the three blue circles always intersect at H. This conjecture is rather easy to prove. A circumcircle is a circle that is the circumscribed circle of a triangle. In other words, all the vertices of the triangle lie on the circle. Hence, H is a vertex of all three triangles besides triangle ABC, then the three circumcircles should intersect.
Notice that when H and C are at the same point it looks as if three of the circles have disappeared. In actuality only 2 have disappeared. The below circle is the circumcircle of triangle ABC and HAB. The two circles that have "disappeared" are the circumcircles for triangle HAC and HBC since these triangles are no more than straight lines.