 EMAT 6690
EMAT 6690
Essay 2
Pedal Triangles
and Similarity
by Kimberly Burrell,
Brad Simmons, and Doug Westmoreland
If we have a triangle ABC and a point
P, we can begin to construct the pedal triangle of triangle ABC
for the pedal point P by constructing a line perpendicular to
a side of the triangle and passing through the pedal point P.
Likewise, if we now construct perpendiculars to the other two
sides and also passing through the pedal point P, then we will
have three points of intersection. If we connect these three intersection
points ( intersection of the perpendiculars with its respective
side of triangle ABC) with segments, then we have the pedal triangle
for triangle ABC and pedal point P.
For a GSP script that can be used to
construct a pedal triangle please click
here.
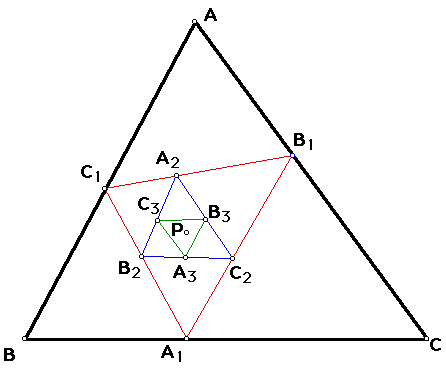
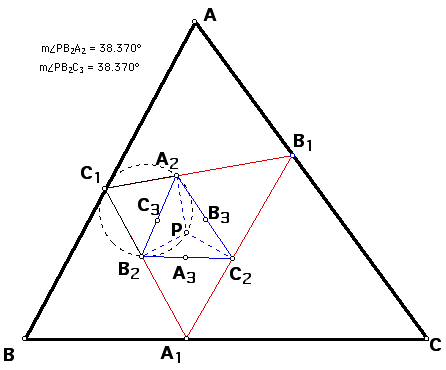
Consider triangle ABC and a point P
located inside the triangle. Construct the red pedal triangle
A1B1C1. Now using the same pedal point P, construct the pedal
triangle for A1B1C1.
This is the blue triangle A2B2C2. Now
using the same pedal point P, construct the pedal triangle for
A2B2C2.
This is the green triangle A3B3C 3.
Triangle A1B1C1 is the first pedal triangle,
triangle A2B2C2 is the second pedal triangle, and triangle A3B3C 3 is
the third pedal triangle for the triangle ABC and the pedal point
P.
Theorem
The third pedal triangle is similar
to the original triangle.
The proof of our theroem above becomes
apparent if we recognize that the point P lies on the circumcircles
of all of the triangles AB1C1, A2B1C2, A3B3C2, A2B2C1, and
A3B2C3.
For a GSP script that can be used to
construct the circumcircle of a triangle please click
here.
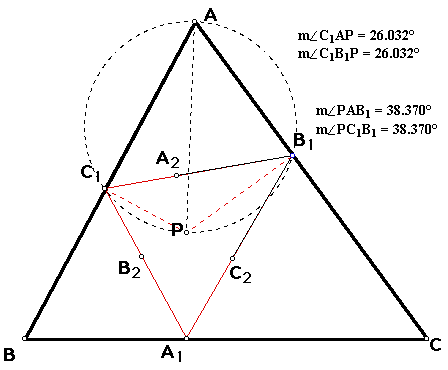
If we stratigically join point P to
A and likewise point P to other vertices in our triangles below,
then we can see
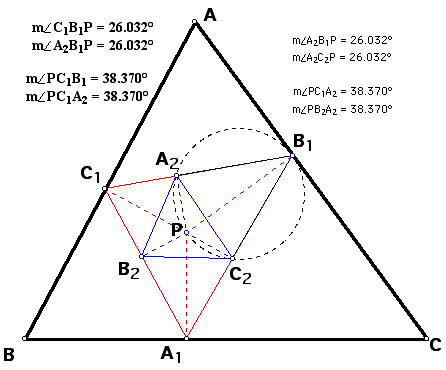
angle C1AP = angle C1B1P = angle A2B1P =
angle A2C2P = angle B3C2P =
angle B3A3P
and
angle PAB1 = angle PC1B1 = angle PC1A2 =
angle PB2A2 = angle PB2C3 =
angle PA3C3.
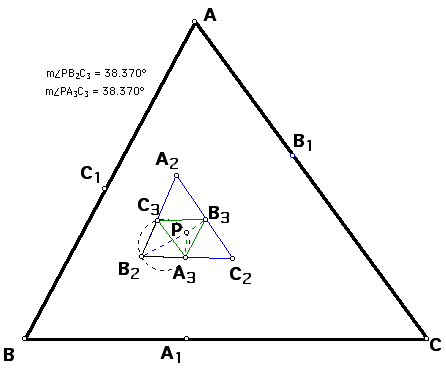
Although the GSP sketch shows that
the angles below are equal. No amount of measuring is proof in
itself. Each of these angles below that are shown to be equal
to each other by measurement, are inscribed in the same circumcircle.
They also subtend the same arc of the circumcircle. Therefore,
they are congruent angles.
 For a GSP sketch of this figure that
can be manipulated please click
here.
For a GSP sketch of this figure that
can be manipulated please click
here.
 For a GSP sketch of this figure that
can be manipulated please click
here.
For a GSP sketch of this figure that
can be manipulated please click
here.
 For a GSP sketch of this figure that
can be manipulated please click
here.
For a GSP sketch of this figure that
can be manipulated please click
here.
 For a GSP sketch of this figure that
can be manipulated please click
here.
For a GSP sketch of this figure that
can be manipulated please click
here.
 For a GSP sketch of this figure that
can be manipulated please click
here.
For a GSP sketch of this figure that
can be manipulated please click
here.
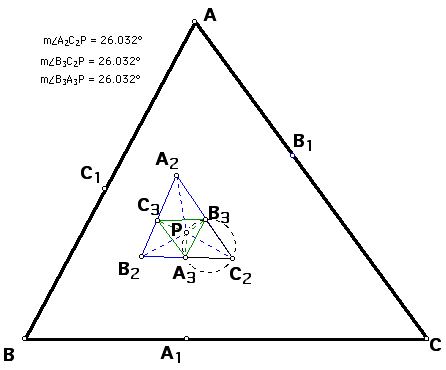
Since angle C1AP = angle B3A3P and angle PAB1 = angle PA3C3
then by angle addition angle A of triangle
ABC = angle A3 of
triangle A3B3C3.
Likewise it can be shown that angle
B = angle B3 and
angle C = angle C3.
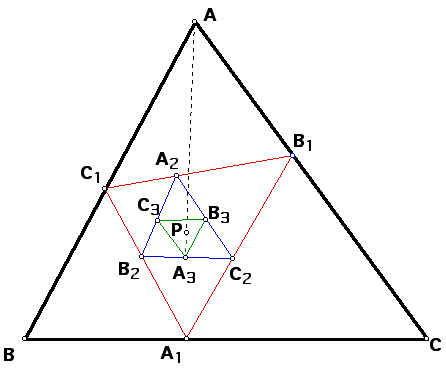
Therefore, by angle, angle similarity,
triangle ABC is similar to triangle A3B3C3.
Conjecture: the sixth pedal triangle is similar
to the original triangle. Furthermore, any multiple of three pedal
triangle is similar to the original triangle.
Conjecture: the n-th pedal n-gon of any
n-gon is similar to the original n-gon.
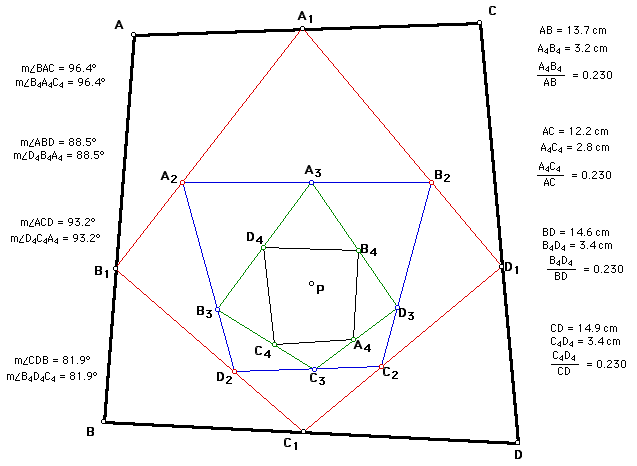 These conjectures can be investigated
using the Geometer's Sketch Pad.
For a GSP sketch of a quadrilateral
and its 4th pedal quadrilateral please click
here.
For a GSP script that will construct
the 4th pedal quadrilateral for quadrilateral ABCD and pedal point
P, please click
here.
These conjectures can be investigated
using the Geometer's Sketch Pad.
For a GSP sketch of a quadrilateral
and its 4th pedal quadrilateral please click
here.
For a GSP script that will construct
the 4th pedal quadrilateral for quadrilateral ABCD and pedal point
P, please click
here.
Return









