

Assignment 2 Sandy Cederbaum
By replacing
each x in ![]() by (x-4),
we see that the red graph appears to be a horizontal
transformation of our original graph. The transformation shifts
the purple graph 4 units to the right.
by (x-4),
we see that the red graph appears to be a horizontal
transformation of our original graph. The transformation shifts
the purple graph 4 units to the right.
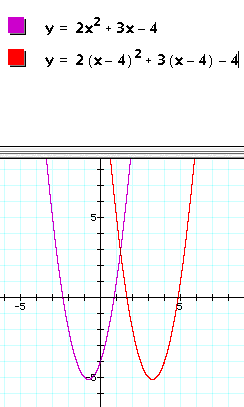
Try this: Plug in 0 for x in the purple equation. Now plug in 4 for x in the red equation. What do you notice? Find another value of x for each of the above equations that will do the same job. Can you find a value of x for each of the above equations that will give you the SAME Y-VALUE generated by our first trial of x=0 and x=4?
You should already have a good idea of how to move a graph to the left. Think about how you might translate the purple graph in order to shift it up and to the left. Change the equation to move the vertex of the purple graph into the second quadrant? Here is the big hint to help you move the graph vertically...Which variable will you ADD to or SUBTRACT from in order to make the graph go up and down? Click here in order to see the solution.
Can you change the equation to produce a graph concave down that shares the same vertex? (Hints: You want all of the y-values to be OPPOSITE, and it might be helpful to find the vertex). Click here in order to see the solution.
You have now had the opportunity to see translations of a quadratic function in a slightly different light. The concepts that you have just worked with should help you become a little more intuitive when faced with a problem that involves shifting graphs around the Cartesian plane.