as illustrated below, we can create
a system of three equations using three known vertices (-1,0),
(0,1), and (1,0).In order to find the locus of the vertices of the set of parabolas
graphed from as illustrated below, we can create
a system of three equations using three known vertices (-1,0),
(0,1), and (1,0).
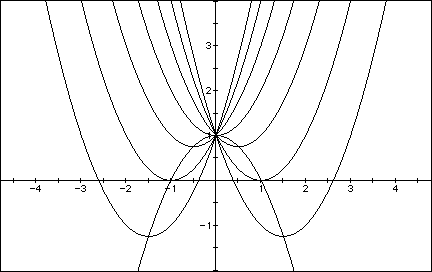
Assuming that the locus is parabolic in shape, and ignoring the
fact that simple translations of the graph of 
would lead us to the conclusion that we are dealing with 
, we can create the following system of equations:
For x=-1 and y=0 ,
For x=0 and y=1,
For x=1 and y=0,
Substituting c=1 into the other two equations we have
, therefore a=-1. Substituting a=-1 into any of the above equations gives us b=0. If we plug this information into our standard form equation for a parabola
, we find our equation for the locus of the vertices of the set of parabolas graphed from
to be
.
