This investigation begins with the following problem.

Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.

The red circle is our goal. It is tangent to both of the given blue circles.

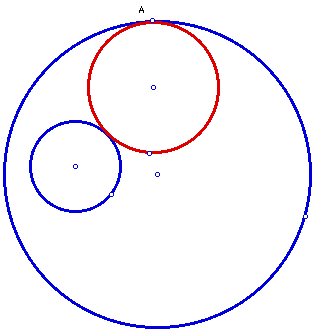
We can construct this circle using a GSP script in order to delve deeper into the problem. Dr. James Wilson from the Department of Mathematics Education at the University of Georgia describes the construction as such:

1. Construct a line through the center of the circle with the designated point of tangency.

2. Construct a circle of the same radius as the second of the given circles with the designated point as center. This can be accomplished by constructing the radius r of the second circle and then creating a circle using center A and radius r.

 

3. The intersection of the line and circle will allow construction of the base of the isosceles triangle and hence allow location of the center of the desired circle.

The Following GSP script demonstrates the above construction. Move circle c2 around and make some observations about the points of tangency when c2 is inside c1, outside of c1, and overlapping c1. Observations?

There are several more tangent circles that have not yet been discussed. For example, we have not yet discussed the circle internally tangent to c1, but externally tangent to c2 as illustrated below:

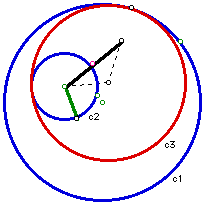
The Following GSP script demonstrates the above construction. Move circle c2 around again and make some observations about the points of tangency when c2 is inside c1, outside of c1, and overlapping c1. Observations?

We have generated two families of tangent circles using the two different constructions. Each family has five different configurations for the circle tangent to two other circles. Have we exhausted the possibilities? More?

The tangent circle investigation is rich with problems and we have only begun to scratch the surface. I hope this exploration serves as a good springboard from which one can continue to investigate the relationships of these families of circles.