There are endless investigations to be explored with respect to the polar equation . For example, we could fix a and b, and investigate what happens to the equation as k varies. Try fixing b and k, and allowing a to vary, or fix a and k, and allow b to vary. You might try these using an application such as Graphing Calculator (NuCalc for IBM compatibles) in order to get a better feel for the graphs of an equation of this form.

We will look at some specific cases of this polar equation for when a and b are equal, and k is an integer. We will compare this graph to the graph of for various values of k, and we will explore the implications of using the sine function rather than the cosine function in this family of polar equations.

For the specific case where a and b are equal, and k is an integer, we get a graph commonly referred to as the " n-leaf rose."

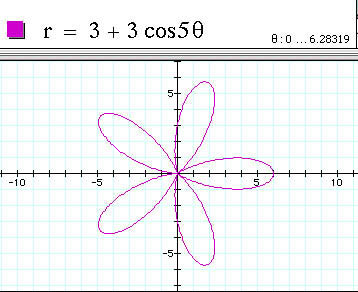
This family of graphs has two interesting characteristics. To see the first, we can vary the value of k in the equation .

For k=0:

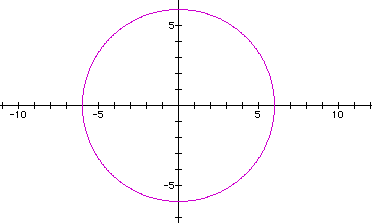
For k=1

For k=2

For k=3

For k=4

How many leaves would you expect the equation to have? Verify.

Now let us use the above four leaf rose and change the value of a and b to see if we can find further patterns in the behavior of this family of graphs.

The graph above is of , where a and b are equal and vary from 0 to 5. What can you determine about the graph where a and b=0. What can you determine about the relationship between the value of a and b, and the distance from the origin to the end of a leaf? Conclusions.

Comparing the above graphs with graphs of , we can look at the following example where k=4, and a and b=5:

What do you notice about the number of leaves on the graphs? What is the relationship of their "leaf radii"? Does your conjecture hold if there are an odd number of leaves? Conclusions.

Finally, what are the implications of using the sine function in these graphs rather than the cosine function? Look at the following examples:

For a and b=2 and k=1

For a and b=3, and k=2

For a and b=3, and k=4

For a and b=4, and k=7

It would appear as though there is some kind of rotation occurring in these graphs. Does this rotation appear to be the same in each case? Can we determine the amount of rotation that has taken place in each case? Discussion.

There is a great deal more exploration to be done even with this very specific family of polar equations. Find and investigate two more interesting characteristics about this family of equations.