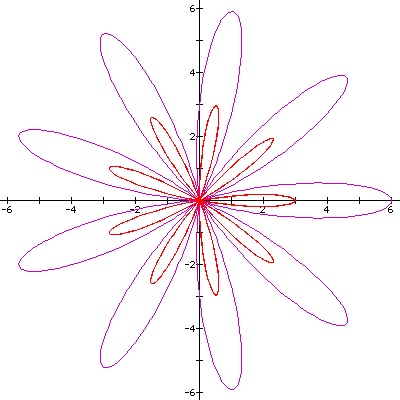

Looking at another set of graphs where a and b=3, and k is odd (k=9 in the case above), we notice that the number of leaves in the two graphs is the same. Verify that this is true for other sets of graphs with odd values of k. The "leaf radii" still appear to be in a 2 to 1 ratio. Does this make sense from our earlier argument?